- 本日の作業内容
- Tukey (テューキー)法
多重比較を行う手法はいくつも提案されています.その中で,この授業では検出力が高く,かつ,バランスが取れているとして定評のあるテューキー法について実際に作業してみます.なお,厳密には各群のデータの個数が同じ場合をテューキー法と言い,群のデータの個数が異なる場合にはテューキー-クラマー法と言いますが,まとめてテューキー法と呼ばれることも多いです.
テューキー法で必要になるのは分散分析でも使用した群内平方和から求める分散 VW (分散分析の回のPDF資料では表3の vw2 とある群内変動の不偏分散)とステューデント化された範囲の表より得る q です.それらについて順に説明します.
- 群内の不偏分散
エクセルで分散分析を行うと得られる分散分析表の「分散」とある内の「グループ内」の方です.各群の中でのデータのばらつきを表します.
この値は独自に求めることも可能ですが,多重比較を行う前に分散分析を行っておけば簡単に求められますので,せっかくですからそのようにしましょう.
- ステューデント化された範囲の表
WindowsのExcel版はこちらです.これは次に説明する臨界差を出すために使用されます.通常の表計算ソフトではこれに関する関数は用意されていません.専用の統計解析ソフト(例えばRなど)を用いれば標準で入っています.
既存の表を使用しますので,危険率 p の値を計算することができません.あらかじめ想定する検定の水準(α が.05もしくは.01)に対応した部分を見て行います.また,表は群の数と自由度で q の値を探すことになっています.自由度は群内の自由度ですので,分散分析表の自由度のグループ内の方です.
- 臨界差 HSD
次に臨界差を VW と q から計算します.求め方は資料の式(4)もしくは(5)です.各群のデータの個数が等しい場合には式(4)を,異なる場合には式(5)を使用してください.
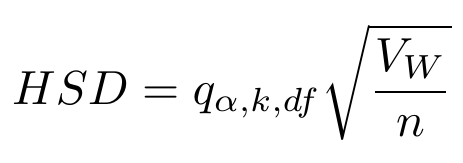
(4) 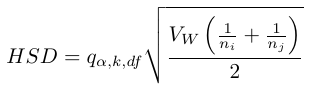
(5) ここで,データの個数 ni と nj ですが,各群の平均値の差についてそれぞれ議論しますからグループAとグループBの平均値の間の差を議論する場合には ni と nj はそれぞれの群のデータの個数となります.
- 群内の不偏分散
- 例題
- 分散分析
まず前回使用したデータを再び使用しましょう.分散分析もすでに先週行っています.
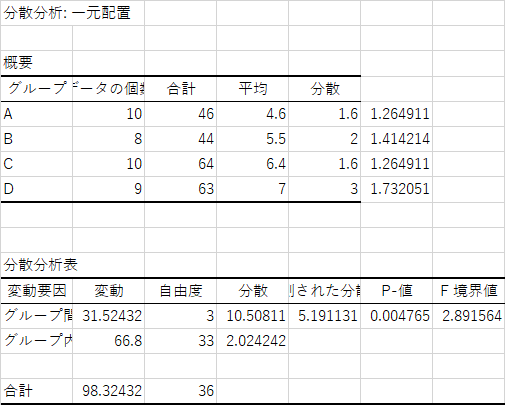
図1 サンプルデータの分散分析表
図2 サンプルデータのグラフ - 表の準備
まず,各平均値の間の差を表にします.このとき,データの並びは平均値の小さい順とします.このサンプルでは最初からそうなっていますが,実際のデータでも並べ替えることをしてください.その方が後で見やすい表になります.
表1 平均値の差の表
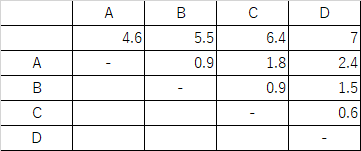
それぞれの群の間の差を総当りで計算しますが,差は表の右上半分だけで構いません.正の値のところだけです.
- 臨界差の計算
分散分析表からまず VW の値を確認しておきましょう.VW = 2.024 です.そして群の数 k は 4 で,自由度 df ですが,全データの個数 N が 37 ですから,df = N - k = 33 となります.スチューデント化された範囲の表には自由度 33 の欄がありません.そういう時はその値よりも小く,かつ,最も近い値を選んでください.今回は 30 となります.そうすると,水準 α = .05 のときで 3.85,α = .01 ならば 4.80 です.
以上で,値の準備は完了です.後は,データの個数が 8 個から 10 個なので,臨界差 HSD を計算する際に ni と nj にそれらの値を適宜使用します.
- 臨界差の表の作成
まず,α = .05 の時の臨界差の表を作ってみました.この表2では,作成が楽になるように,左上に qα,k,df の値を入れています.また,データの個数も上に付けています.それにより,ドラッグ操作で表の空欄を埋めることが簡単になるからです.具体的には授業で説明します.
表2 α = .05 の時の臨界差の表
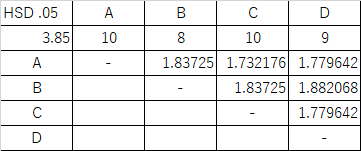
表2の臨界差の値より表1の平均値の差の方が大きければその差は有意であることがわかります.表1では一番右上のセルが最も大きな値になることは自明ですので,そこのセルからだんだんと左方向や下方向に目を向けて行くことで,どこまで有意な差があるのかがわかります.
データが多くなってくると目で見比べるのは大変でしょうから,そういう場合は関数を使用することもできます.表のそれぞれの位置に対応する場所に次のような if() 関数を入れてみます.
=IF([差のセル]>[HSDのセル],1,0) もちろんセルの番地は自分の表に合わせてください.これにより,差の方が大きい場合には1が,そうでない場合には0が表示されます.
表3 平均値の差と HSD の比較の表
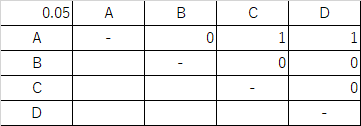
元々分散分析を行った時の危険率 p は .0048 でしたので,α = .01 でも有意な差が得られることが予想されます.そこで,同じ操作を α = .01 に対しても行うと,結果としては以下の表4のようになりました.
表4 α = .01 の時の臨界差の表
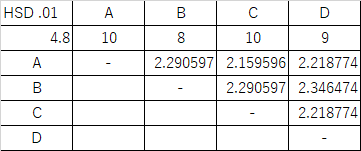
群 A と D の平均値の間には危険率 .01 未満の有意差があることがわかりました.
- 結論
テューキー-クラマー法による多重比較によって,A から D の群の平均値の間に以下のような有意差があることがわかりました.
A と D の平均値の間には p < .01 の,A と Cの平均値の間には p < .05 の有意差が見られた.
- グラフ
今回の多重比較の結果は図3のようなグラフにまとめられます.
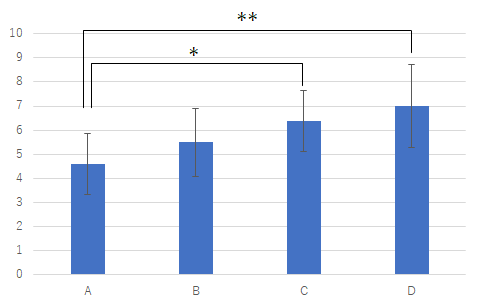
図3 サンプルデータの結果のグラフエラーバー付きのグラフにすることで,棒とエラーバーの重なり具合が見えるので感覚的にもよくわかります.
- 分散分析
- 演習
- Jリーグのゴール数(順位)
先週の実習で使用したJリーグの上位,中位,下位の得点力についてのデータで多重比較を行ってみましょう.結果は図4のようなものでした.
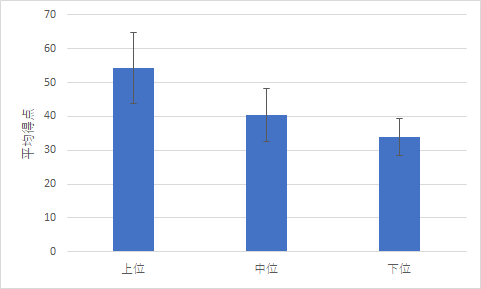
図4 2022年度J1リーグの順位グループ別得点 - コロナ死者数
こちらも先週使用したコロナ死者数の地域の傾向について,多重比較を行って有意な差を確認しましょう.
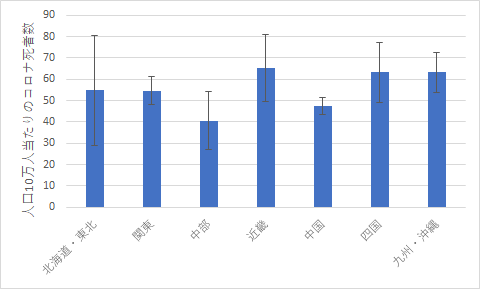
図5 地方別コロナ死者数 - Jリーグのゴール数(季節)
先週の宿題で使用したJリーグの時期別のデータについても多重比較を試してみましょう.
- おまけ
この授業のレポート提出に関して,提出時期(時間)がなんらかの影響を持っているかと推測し,添付のような表にまとめてみました.表は課題の提示日ごとに,日曜日までに提出した人,月曜日提出の人,火曜日のお昼までに提出の人,火曜日の午後(12:00−13:00)に提出した人の人数と,その内合格点に達しなかった件数です.分析してみましょうか?
- Jリーグのゴール数(順位)
- 次回の予習範囲
まずゴール数について,各月別のデータを確認してみましょう.
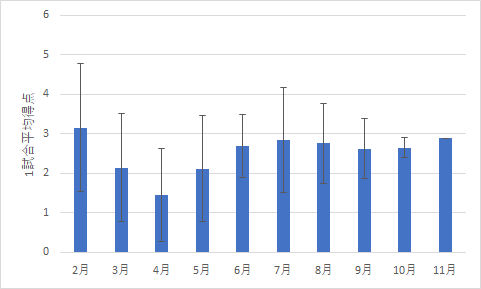
上の図を見ると,春にゴール数が少い時期があるようです.
そこで,どう季節を区切るかが問題になりそうです.そこで,以下のように3種類の区切り方をしてみました.
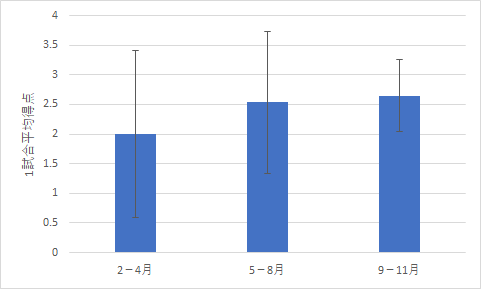
|
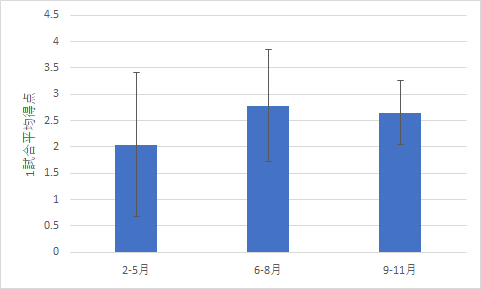
|
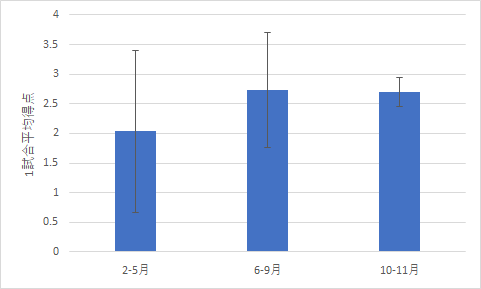
|
| 夏場を5月から8月とした場合 | 夏場を6月から8月とした場合 | 夏場を6月から9月とした場合 |
| p = .15 | p = .045 | p = .048 |
どのように季節を区切るかについては恣意的な操作が入ってしまうので,なんとも言えませんし,あくまでW杯のために変則的になってしまった昨年1年のデータなので,何も具体的なことは言えないかもしれません.一応,Jリーグがシーズン移行を検討している理由の一つに夏場の疲労によるパフォーマンス低下で失点が増えることが挙げられています.今回のデータでも夏場のゴールが多いことは確認できますが,秋もゴールが多いというこも言えるかもしれません.ということで,詳しいことはこの後の多重比較でも考えてみましょう.
さて,皆さんに出していただいたレポートですが,例によって残念なものが幾つか見られました.このところ行っている統計的仮説検定ですが,これまでに行った t 検定や分散分析というのは,複数の平均値の間に有意な差があるかどうかを検定するものでした.そのときに,当たり前ですが,基本的なことは平均値を比較するということです.例えば,20歳男子大学生の「身長」の平均値と「体重」の平均値の間に有意な差があるか,比べることに意味はあるでしょうか?
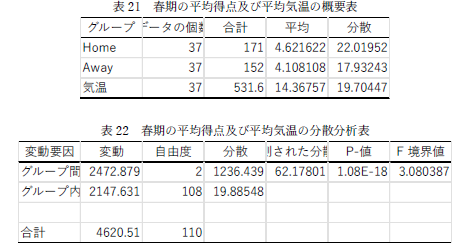
|
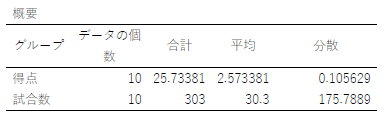
|
上の表を見てどうでしょうか?私は,絶句しました.
ということで,グラフでもそのようなものはありましたし,比較するものがきちんと考えられていないものも多く出てきました.
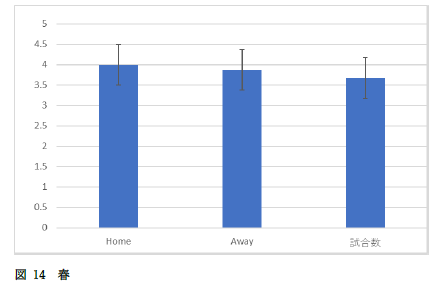
|
どうしてこの3つのデータの高さを比べようということになるのでしょうか? |
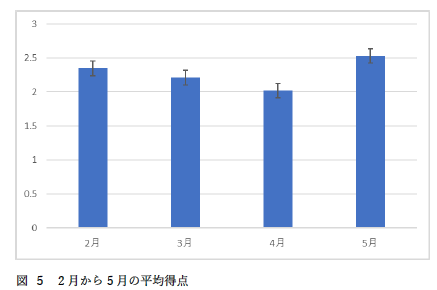
|
単純に月ごとの平均値を比べているだけですよね? |
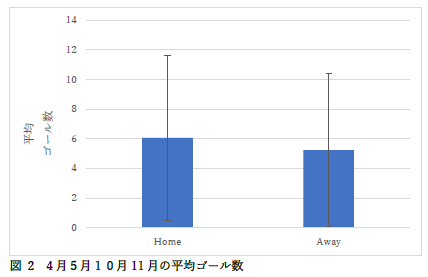
|
分散分析というのは3つ以上の平均値を比較するものですが? |
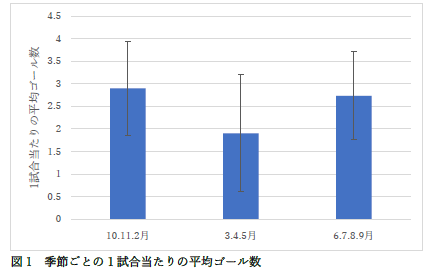
|
左のように2月を11月などと一緒にしているものが多く見られました.サッカーの題材を無理矢理やってもらっているので,あまり細かいことまでは減点したりはしないのですが,シーズン最初の2月と最終版の11月は選手の調子も変わっていたりするので,一緒にすべきでは無いと思います. |
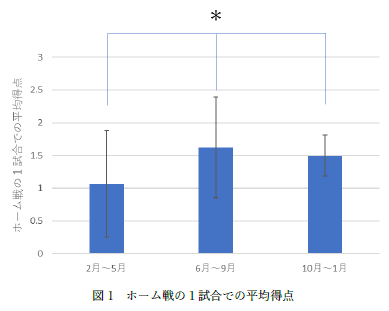
|
前回説明しましたが,分散分析だけでは特定のデータ間についての議論はできません.今回の多重比較で学習します. |
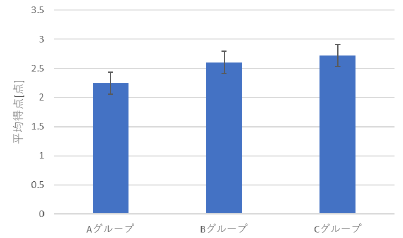
|
左の図のエラーバーは実際の誤差にはなっていないようです.例によって,EXCELの「標準偏差」を選んでしまって,これらの3つの値の標準偏差が表示されたようです. |
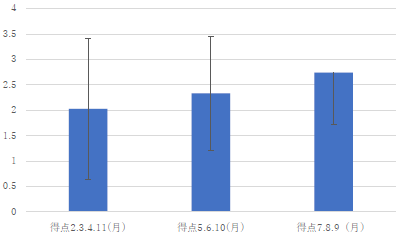
|
右端のデータのエラーバーの上側が付いていませんね. |
分散分析表に関しても惜しいものが以下のようにありました.注意してください.
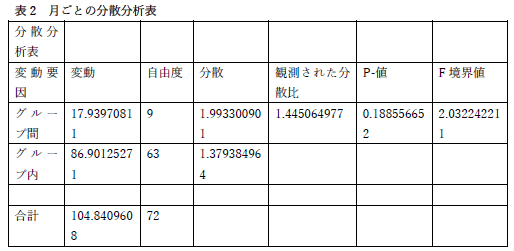
|
以前にも言及してはいたのですが,表を貼り付けてサイズを調整する際に,単純に横幅を縮めてしまうと,左のように数値が途中で改行されます.数値の改行はありえませんので,そこは注意してください. |

|
分散比が 3.22 で,境界値 F が 3.13 ということは,このデータでは有意な差があることを示しています.ところが,危険率 p の欄を見ると,0.460となっています.おそらくコピペをしたのではなく,自分で数値を入力したと思われますが,その際にミスりましたね. |
分散分析について学習しましたが,結局分析とはどのような作業をすることなのか,統計的仮説検定について,もう一度よく見直しておいて下さい.
資料を参考に予習してください.
分散分析によって,データの平均値の間に有意な差が検出されたとしても,どのデータの間に有意な差があるのかはわかりません.そのため,各群の平均値の間の有意差を具体的に検討する手法として多重比較があります.今回はその中でもテューキー法と呼ばれる方法を実際に試してみます.ただし,これまでと異なり,表計算ソフトにはそれ用の関数は用意されていません.原理に即して手作業で行うことになります.
次回は2元配置分散分析について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは翌週火曜日の13:00までです.よろしくお願いします.
Back