- 本日の作業内容
- 二重ループおよび二重配列について
- forループの使い方(数値計算編)
- 宿題
先週までの復習課題で意図的に多重配列及び多重のループを使うようにしていた。詳しく習っていない段階だったので、当然、苦労したことは理解しており苦心の作のスクリプトを拝見させていただいた。中には、かなりの技巧を駆使して処理方法を工夫した例もあり、一部に高いスキルを持った人がいることも分かった。しかし、まだ、多くの人が解決への道筋を見いだせていないようなので、今回もループに関する復習を行う。特に、課題で使用した二重ループとそれに関連した多重配列の扱いの例について示す。
教科書ではループとしてはwhileの例が多く出ており、また、eachメソッドなどでforやwhileが明示的に現れていないような例が紹介されたりしている。中級以上の実力が伴ってくるとそれらのありがたみが分かるが、とりあえず、単純なforループの使用を考える。以前にも示したが、forの利点はwhileループから変数の初期化、次の要素の取り出し、終了条件などを省略できるので、スクリプトがすっきりすることが多い。
基本的な使用法は
for i in 0..9
puts i
end
のような表現になり、上のスクリプトを実行すると0から9までの数を順に出力する。
さて、実際の二重ループであるが、ある行列の転置行列を求めるスクリプトの例で紹介する。元の行列として、
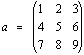
があるとすると、その配列表現は
a = [[1,2,3],[4,5,6],[7,8,9]]
のようになる。その場合、行列の要素aijが配列要素a[i-1][j-1]に対応する。転置行列をbとすると、要素の関係はbij = aji であるので、その変換スクリプトは以下のようになる。
a = [[1,2,3],[4,5,6],[7,8,9]]
b = [[],[],[]]
for i in 0..2
for j in 0..2
b[i][j] = a[j][i]
end
end
p b
実行の順序としては、 i = 0 がセットされ、次に j = 0 がセットされ、順に j = 1, 2, 3 と増えていく。その次に、 i = 1 に上がり、再び、jの値が0から3まで実行される。後は同じように順番に実行され、全てのiとjの値について実行するようになっている。二つの変数を順に変化させるためにfor文を二つ必要とするが、その形式は入れ子と呼ばれるものになり、for..endの中にもう一つfor..endが入るので、二重になる。必要に応じて多重化はいくつでも可能である。
上記のように、あらかじめ始めと終わりが決まっている場合にはforループは非常にすっきりとしたスクリプトになるので、使い方によってはずいぶんと楽にスクリプトが書けるようになる。復習課題も同じような二重のforループを使用すると簡単である^^)
Rubyはテキスト処理に威力を発揮するスクリプト言語なので、教科書には役に立つ例として電話番号検索のためのスクリプトを軸として各種の機能が紹介されている。しかし、数値計算に用いることも別に問題ないし、本学科の授業構成を考えると、数値計算のアルゴリズムの検討は今後も重要な課題である。特に、後期から始まるC言語の授業は数値計算を通してCを理解することが目的とされているので、その少し前に学習しておくのも予習としてうってつけである。
さて、ではどのようなスクリプトが良いか、となると、今後も頻繁に使われることが予想される定積分を求める例が考えられる。以下に示すのは非常に単純な関数の定積分であるが、自分で中身をいじるとそれなりの関数も計算できるようになる。ここでは関数f(x)=x^2について考える。
まずは、定積分の概念であるが、考える範囲についての関数の値を連続的に足しあわせて面積を求めるようなものである。一番単純に考えると、下の図に様に棒グラフの面積を足しあわせることにより計算できる。
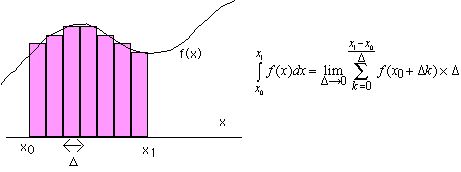
それをスクリプトにしたのが、以下の例である。ここではxの値が0から2までの範囲で積分する。
x0 = 0.0
x1 = 2.0
n = 10.0
delta = (x1 - x0) / n
integral = 0.0
def f(x)
x**2
end
for xx in 0..n-1
integral += f(xx * delta) * delta
end
printf ("Integral = %f\n", integral)
ここでは、積分範囲を10の領域に分けて足しあわせることとした。for文においては、順番に変数の値を1ずつ増やすことしか出来ないので、増分の設定には注意が必要である。ここでは、Δずつ増えていくので、ループの中の式の引数は変数×Δの形式としている。実際の定積分は自分で計算してみれば分かるように8/3である。上記のスクリプトの実行結果は2.28であり、だいぶ精度が悪い。試しにnの値を増やしていくとどうなるか、実行してみよう。
上のスクリプトの精度が悪いのは実際には下の図のように高さに問題のある棒グラフで近似したからである。
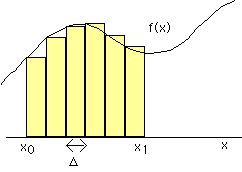
次の図のように台形で近似して面積を足しあわせるとだいぶ正確になりそうである。
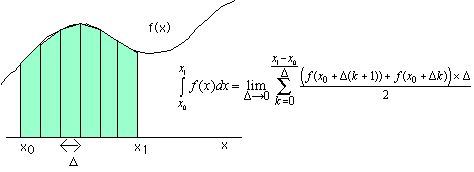
実際にこれはSimpsonの台形公式というものであり、数値計算で良く用いられる方法である。台形の面積は、(上辺+下辺)*高さ/2となるので、そうなるようにスクリプトを変更したものが以下の例である。
x0 = 0.0
x1 = 2.0
n = 10.0
delta = (x1 - x0) / n
integral = 0.0
def f(x)
x**2
end
for xx in 0..n-1
integral += (f((xx + 1) * delta) + f(xx * delta)) * delta / 2
end
printf ("Integral = %f\n", integral)
この場合の計算結果はn=10に対して2.68であり、かなり改善されていることが分かる。nをさらに増やしてみるとどうなるか、試してみよう。
関数の定義さえしっかりやっておくとこのスクリプトは結構使い回しが効きそうである。他にも、数値計算で作業が簡単になる例はたくさんあるので必要に応じて自分で試してみるのがおもしろいかもしれない。ただし、解析的な計算(たとえば導関数を求める様なケース)は計算機は苦手である。あくまで、数値計算が楽に出来る、ということを覚えておいた方がよい。(もちろん、解析的な計算が出来るようなプログラムもあるが、とりあえず無いものと思っておく方がよい。)
教科書の例題をずっとまじめにやってきた人はかなり力が付いてきていると思われる。入門の割には相当高度な技が使われており、しかも、Rubyの特徴を一通り網羅したような内容になっているので、使いこなせれば相当なものになる。しかし、その分、初心者が見てスキッと理解することが困難になっているのは実感しているだろう。そこで、自分でさらに学習を進めることはもちろん構わないが、今日のところで、1章を終わることにし、次週からは2章に移りふたたび基礎から学習する方が良さそうだと判断した。
今日の範囲にはインスタンス変数やクラス定義、ブラックボックス化、継承とインクルードと言ったそれなりに重要な概念が目白押しである。理解するに越したことはないが、現段階では一通り試してみて、教科書のスクリプト例の実行を通して、テキスト処理の便利さを実感する程度でよい。また、このほかの初歩的なテキスト処理として昨年度の授業で行った表計算処理および結果を見栄えよく出力する方法などもあるので、参考にして欲しい。
作業1
2.に挙げたループの実習を自分で試してみること。
作業2
3.に紹介した定積分の数値計算の例題も試してみること。
作業3
教科書の電話番号検索スクリプトも試してみること。
授業の終わり頃に次回までに提出する課題を発表するのでアナウンスに注意すること。また、発表されたら課題を表示するためには、一度このページを再読み込みする必要があるのでNetscapeのボタンをクリックする。そうしないと、課題のページは表示されない。
目次ページに戻る