100 から 200 の範囲の整数を乱数により2個発生させて,その範囲の数の約数をすべて表示するプログラムを作成しましょう.
168: 1 2 3 4 6 7 8 12 14 21 24 28 42 56 84 168 169: 1 13 169 170: 1 2 5 10 17 34 85 170 171: 1 3 9 19 57 171 172: 1 2 4 43 86 172 173: 1 173 174: 1 2 3 6 29 58 87 174 175: 1 5 7 25 35 175 176: 1 2 4 8 11 16 22 44 88 176 177: 1 3 59 177 178: 1 2 89 178 179: 1 179 180: 1 2 3 4 5 6 9 10 12 15 18 20 30 36 45 60 90 180 181: 1 181 182: 1 2 7 13 14 26 91 182 183: 1 3 61 183 184: 1 2 4 8 23 46 92 184 185: 1 5 37 185 186: 1 2 3 6 31 62 93 186 187: 1 11 17 187 188: 1 2 4 47 94 188 189: 1 3 7 9 21 27 63 189 190: 1 2 5 10 19 38 95 190 191: 1 191 192: 1 2 3 4 6 8 12 16 24 32 48 64 96 192 193: 1 193 194: 1 2 97 194 195: 1 3 5 13 15 39 65 195 196: 1 2 4 7 14 28 49 98 196 197: 1 197 |
500 から 999 の間の数で約数の個数が最も多いものを探し,その約数を表示するプログラムを作成しましょう.
The number having max divisors between 500 and 999: *** Number of divisors: 32 Divisors: 1 2 3 4 5 以下略 |
最大の約数を持つ数を探し出して表示した後で,最後の行の表示用にもう一度約数を探して表示します.プログラミング入門IIで扱うリストを使うとその必要はありませんが,処理はさらにややこしくなります.
1000 以下の素数をすべて表示するプログラムを作成しましょう.
Prime numbers below 1000 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 ・・・ 以降 略 |
約数の個数から判断する方法と,約数が見つかるとすぐに次の処理に移って時短を行う方法とがあります.
ループを途中で中断する break を使用すると処理が早く終わるものがあります.上の2つの解答例の処理時間を比較するプログラムも作ってみました.興味ある人は自分で確認してみてください.ただし,1回目は読み込み等でいろいろ時間がかかるものがあるので,2回以降実行して確認することをお勧めします.
自分自身を除く約数の和が自分自身に一致する数を「完全数」と言います.例えば,6 は約数として 1, 2, 3, 6 を持ちますが,自分自身以外の約数の和は 1 + 2 + 3 = 6 となり完全数です.4桁までの完全数を全て見つけるプログラムを作成しましょう.
Perfect numbers below 10000: 6 28 ・・・ 以降 略 |
10 人の学生さんの英語,数学,物理の各科目のテストの得点を乱数を用いて 1 から 100 の整数で用意し,各学生の平均点,全体の平均点と平均点の最高点,最低点を以下のように表示するプログラムを作成しましょう.
No Eng Math Phys | Total
1 26 28 50 | 34.7
2 71 58 41 | 56.7
3 3 20 79 | 34.0
4 76 79 62 | 72.3
5 8 14 2 | 8.0
6 90 94 72 | 85.3
7 73 90 8 | 57.0
8 69 57 50 | 58.7
9 17 88 92 | 65.7
10 72 34 84 | 63.3
----------------------------
53.6
Best mean score: 85.3
Worst mean score: 8.0
|
円周率は無限に小数部が続く無理数ですが,小数第〇位まで計算した,というような話を聞いたことは無いでしょうか?なぜそんなことができるのでしょうか.ということで,ゼータ関数を変形したオイラー式(下の式)を実際に計算してみましょう.最初の項は 3 ですので,この式は項が増えていくとともに少しずつ値が大きくなり円周率に近づいて行くことになります.どの素数までの計算で 3.14 まで行くのかを調べましょう.
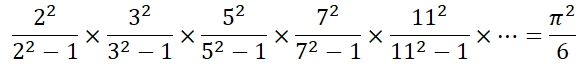
3: 3.0 5: 3.0618621784789726 7: 3.0935921676911455 11: 3.106455392270532 13: 3.1156870779784582 17: 3.1210915695996455 19: 3.1254234128635265 23: 3.1283816940869547 以下,略 |
実際に 3.14159 まで到達するのはものすごく大きな素数までの計算が必要になり,メモリがあふれて Python が固まりますので,今回は 3.14 までとします.
外側のループには while 文を使う方が簡単になるかもしれません.
方法としては,初項はあらかじめ用意しておき,次の素数を見つけるたびに分数をかける,すなわち *= で値を求めていきます.π2 が出てきますので,平方根を求める作業が必要になりますが,import math を置けば,math.sqrt() が使えます.もちろんべき乗の ** .5 でも可能ですが.