- 本日の内容
- 独立性検定
最初は単純に男女の時間数から期待値を求めて独立性検定を行ってみました.結果は3つの表をまとめた以下の表1に示します.
表1 独立性検定
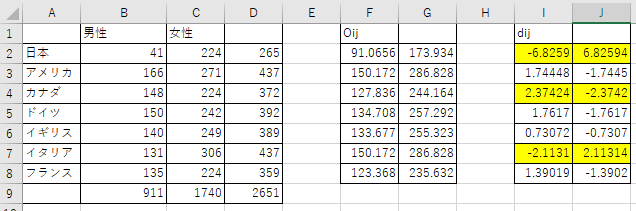
χ2 検定を行う関数 chitest() で確認すると,危険率 p = 1.24 × 10-10 となり,これらの時間数には有意な差があることがわかりました.
時間数をグラフで表すと以下の図1のようになります.
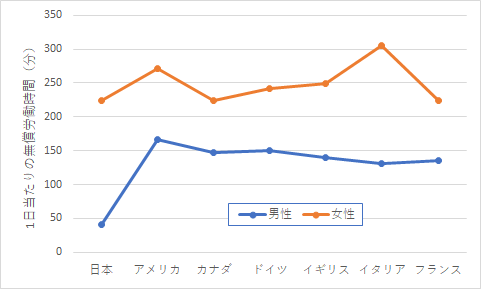
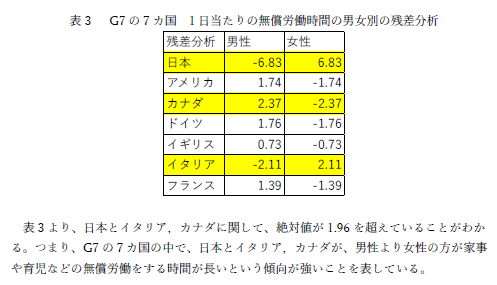
図1 G7各国の無償労働時間の男女の違い - 残差分析
残差分析を行った結果も上の表1の一番右の表にまとめてあります.黄色でハッチングしたところが絶対値が 1.96 を超えているものです.それをみると,日本の男性の従事時間が著しく低いということがわかります.カナダはまだ女性の方が従事している時間は長いものの,G7の中では男性の従事する時間が有意に長いことがわかりますので,日本の女性はカナダに移住すると幸せになれるのかもしれませんね.イタリアも男性の時間が有意に短いのですが,日本人男性の従事時間の少さは突出しています.
- 適合度検定
今回のデータは他にも使い方があるようで,χ2 検定の適合度検定も試してみましょう.これは男女が同じ時間無償労働すると仮定した場合に比較して,どちらかのジェンダーの方が偏って従事しているかどうかを検定するものになります.
男女の時間の比について,グラフと表にまとめてみました.図2と表2を見てください.
図2 無償労働時間の男女比.(a)男性/女性,(b)女性/男性(a) 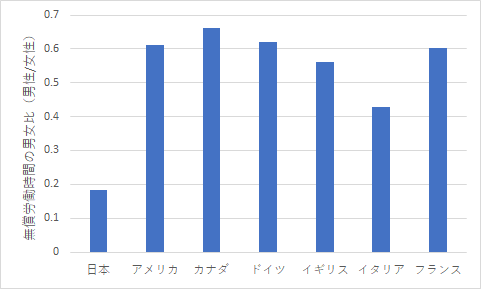
(b) 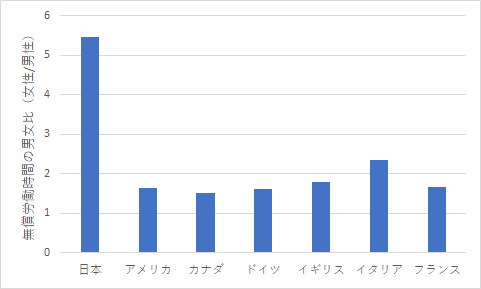
表2 無償労働時間の男女比(適合度検定用).(a)男性/女性,(b)女性/男性
(a) 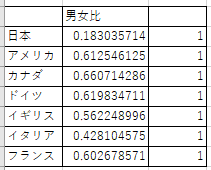
(b) 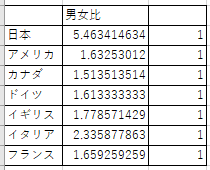
実際に上の表を使用して chitest() 関数を適用すると興味深い結果となります.表2 (a) の方の危険率 p は 0.94 なのですが,(b) では .00057 となり,女性の時間を男性の時間で割った方の比率は有意な差が含まれるという結果になりました.まあ,日本の数値が突出していますからね.0 に近い方の値に外れるよりも,1 よりも大きい値に外れる方が有意な比率の差が出る傾向にあるようです.
- 適合度検定 その2
他にも,男女の時間数がそれぞれ 1/2 になるという期待値に対して適合度検定を行ってみました.表3のようにデータを作ってみました.
表3 無償労働時間の男性負担率
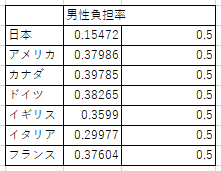
この場合の chitest() 関数による危険率は .998 で結構比率に差があるように見えても,有意な偏りではないということになるようです.女性の負担率で計算しても同じ危険率になります.
- 適合度検定 その3
比率は比率でも,それぞれの国で従事する時間が異なっているので,その時間数の 1/2 となるような期待値を用意するとどうなるかも試してみました.表4を見てください.
表4 無償労働時間の男性負担時間
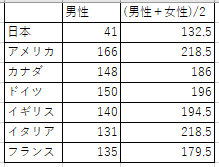
この時の危険率はなんと 4.8 × 10-31 となりました.日本男性のあまりの低さがやはり群を抜いているという結果となりました.
無償労働時間の男女における違いをG7の7カ国についてまとめたものを題材に,日本の現状を確認してもらう課題でした.まとめ方はいろいろとありますが,まずは私の方で行った検定をご紹介します.
まずは検定の名前についてです.

|
Webブラウザでは表現力が足らないのできちんと見えなかったのかもしれませんが,今回の検定の名前は χ2 検定で,ギリシア文字の「χ」が使われています.なお,χ の大文字はただの X になってしまうので,大文字ではなく小文字の χ を使う必要があります. |

|
上でも説明したように x ではありません. |
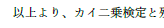
|
「カイ」でもありません. |
次に検定について問題があるものの例です.
|
国別に一対比較をするのではありません. | |
|
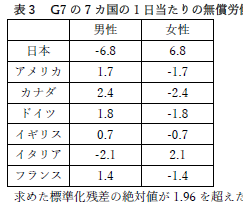
多くの人がここで同じような間違いをしていたのですが,日本とイタリアは男性が負の値で女性が正の値で 1.96 を超えているのに対し,カナダは正負が反対です.カナダにおいても男性の方が時間は長いですが,残差から見ると他の国に対し男性の従事する時間が長いことが言えます. | |

|
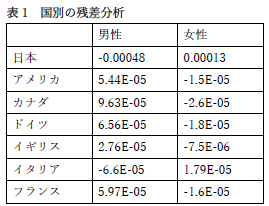
調整済み標準化残差を使用しているので,危険率ではありません.1.96よりも絶対値が大きいかどうかを見ます. | |
|
残差の計算はどうなっているんでしょうか? | |
|
1.96 との大小関係を見るのですから,有効数字としては小数第2位が必要ですよね. | |
最後は文中の英数字の表現に関してです.最後までなかなかなくなりませんでした.
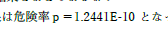
|
p がイタリックになっていないし,べき乗が上付きになっていません.E を用いた指数表現はプログラミング言語や表計算ソフトなどの特殊な用途で使用が認められているもので,文章の中で使用するものではありません. | |
 イタリックになっていないし,添字が下付きにもなっていません. イタリックになっていないし,添字が下付きにもなっていません.
|
||
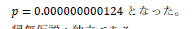
|
こんなに 0 を並べなくても良いように,指数表現があるわけですね. | |
Back