- 本日の作業内容
- 主効果:順位について
上位,中位,下位のグループの得点および失点について有意な差が見られた.
F302 = 3.68, p = .037 - 主効果:得失点について
全チームの得点と失点については有意な差は見られない.
F301 = 8.4 × 10-15, p = 1.0 - 交互作用について
順位グループと得失点について有意な交互作用が見られた.
F302 = 9.08, p = 8.2 × 10-4 - 適合度検定
標準で用意されている chitest() などの関数は「独立性検定」となっていますが,適合度検定はこの関数を使用して簡単にできます.
- サイコロの目の頻度
サイコロを36回振って,それぞれの目が何回出たかを記録するプログラムを Python で作ってみました.以下のプログラムは実行すると,各目が出た回数を画面に表示するとともに,dice.csv ファイルに結果を保存します.
import random import csv result = [[i+1, 0] for i in range(0,6)] for _ in range(36): dice = random.randint(1,6) result[dice-1][1] += 1 for i in range(0,6): print(f'{result[i][0]}: {result[i][1]:2}') with open('dice.csv', 'w', newline='') as f: line = csv.writer(f) line.writerows(result)試しに何度か行ってみたところ,極端なときには以下のようになりました.
1 5 2 5 3 10 4 7 5 4 6 5 EXCEL の方に,データを移しますが,確率的には各目は6回ずつ出るはずですので,下の図のようにデータを用意します.
- chitest() 関数
使用するのは chitest() 関数です.引数仕様は,実測値,期待値の順ですので,それぞれ実測と期待値のセルを選択します.今回の場合だと,結果を危険率 p で返してくれます.この場合は, p = 0.549 となるはずです.
- 検定結果
随分と目に偏りがあるような気もしますが,今回の結果はサイコロの目はそれぞれ1/6の確率で出るという帰無仮説を否定する危険率が .05 を超えていますので,棄却できないことになります.つまり,出た目の割合は有意に偏っているとは言えない,という結論です.
- サイコロの目の頻度
- 独立性検定
独立性検定とは,個々のデータが独立であるか,依存関係にあるかを検定で確認します.独立とはお互いに影響しあわないことで,座標軸の xyz はそれぞれ独立であるとか,よく聞くはずです.数学的には,「直交している」とも言います.
「独立である」とは,データの間に関連は無い,ということです.独立性検定の場合には帰無仮説としては,「独立である(関連はない)」となり,対立仮説が「独立でない(関連性がある)」となるので,ちょっとややこしくなります.
- プラシーボ効果
プラシーボ(偽薬)効果というものがあります.薬理作用が無いにもかかわらず治療薬だとして与えられると患者の症状が良くなる場合があることです.そのため,新薬の開発ではその薬が本当に効果があったのかについて薬理作用の無い物質を投与した場合との効能の違いを見ることが行われます.リンク先の資料の表1および表2のように,新薬と偽薬を投与して改善した人数と変わらなかった人数が出たとすると,この新薬には効果があると言えるかを,それぞれのデータについて独立性検定の観点で議論して下さい.
- 表1のデータについて
表1では実際に新薬を飲んで改善した人,しなかった人の行と,偽薬を飲んだのに回復した人としなかった人の行,それから,改善と変化なしの合計が入力されています.独立性検定の作業は,各欄の実測値から期待値を引いたものの2乗を期待値で割ったものの合計である χ2 を求めることです.
- 期待値
期待値は,あるセルを考えた時,その行の合計とその列の合計を掛けあわせ,全体の合計で割ったものになります.
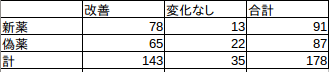
上の表であれば,例えば,新薬の改善(左上)であれば, 143×91÷178 で求められます.表計算ソフトなので,次のようにすればドラッグで他のセルの計算もできます.
= B$4*$D2/$D$4
もちろんセルの記号と数字はそれぞれの環境で異なりますので,自分のセルに合わせて下さい.では,各セルについて期待値を求めましょう.
- chitest() 関数
これでchitest() 関数を使用する準備ができました.どこかのセルで使用して下さい.実測値と期待値はそれぞれ自分が用意したセルを選択します.そうすると,危険率 p が計算されます.今の場合は, 0.065 ということで,それぞれのデータは独立である,という結論になります.実際の意味としては,今回の新薬の効果は有意ではなかったということです.
- 表2のデータについて
ちょっと数値が変わった表2についても検定を行ってみましょう.
- 期待値
- 血液型
PDF資料にある「ある集団の血液型分布」の例を見てみましょう.表は以下のようになっています.
血液型 A O B AB 計 男性 55 22 16 7 100 女性 40 32 24 4 100 計 95 54 40 11 200 χ 2 検定を行って資料の通りかどうかを確認してみましょう.
- 座席位置と成績分布
先日課題として行った計測工学基礎の座席位置と成績ですが,SからEまでの評価の分布について改めて考えてみましょう.リンク先のデータを使用して,いろいろな組み合わせで比率が有意に異なっているのかを確認しましょう.円グラフで表してみるのも,視覚的に分かりやすいかもしれません.
- 試験の有無の効果
同じく計測工学基礎の過去の評価分布について考えます.リンク先のデータは2015年度から昨年度までの評価分布です.年度ごとの特徴としては,以下の表のようになっています.χ2 検定で4つのグループの分布を確認してみましょう.
年度 特徴 2015-2018 大教室で座学.評価は各回の課題と中間試験,期末試験. 2019 720教室で演習形式.評価は各回の課題と3回の小テスト.OS はLinux. 2020 オンデマンド形式.PDF資料とWebページで学習.評価は各回の課題のみ. 2021-2022 オンデマンド形式.PDF資料とWebページ,EXCEL操作に関する動画で学習.評価は各回の課題のみ.
- プラシーボ効果
- 残差分析
残差分析についても,上で行った事例について試してみましょう.計算は授業資料の式 (4) を使用します.
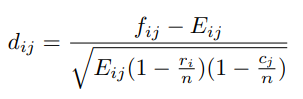
(4) 式 (4) において,f ij が与えられたデータ(頻度)で,E ij は検定を行う際に使用した期待値です.また,r i は行 (row) 全体の頻度データの和,c j は列 (column) の頻度データの和,n がデータ全体の頻度の和です.
dij は調整済み標準化残差などとも呼ばれますが,この絶対値が 1.96 を超えると,その頻度の部分が有意に偏っているという結論になります.標準正規分布の標準偏差は 1 なので,その1.96倍のところが片側 5% になる部分ということです.
前回の分散分析と多重比較の関係のように,この残差分析も χ 2 検定とは独立になっています.正規分布を想定した残差分散を使用しているので,検定で有意差が出なくても,有意な差が見られることがあります.
- 宿題
今回は締切りが変則的でしたので,提出数が普段より少なくなってしまいました.また,先週のものを提出した人が2人いました.出来時代はだいたい良かったと思います.
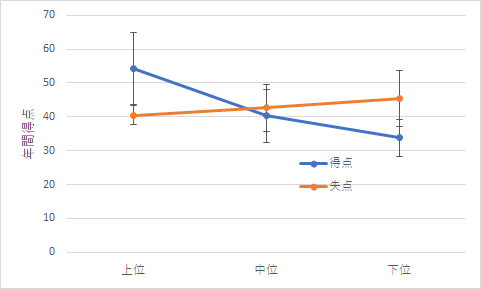
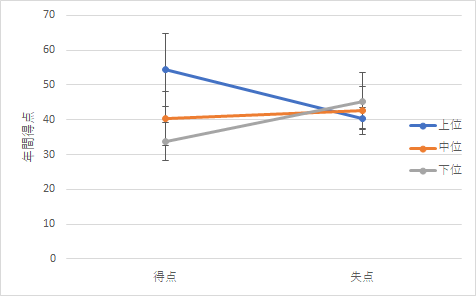
まず,結果ですが,グラフとしては以下の2種類が作れます.
|
|
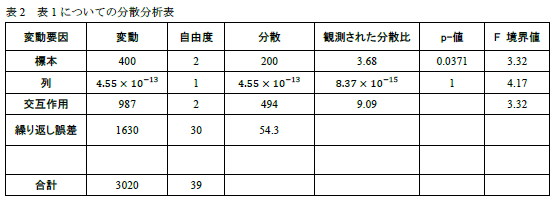
今回の考察をするのには,左側のグラフの方が分かりやすいと思います.分散分析の結果は以下のようにまとめられます.
|
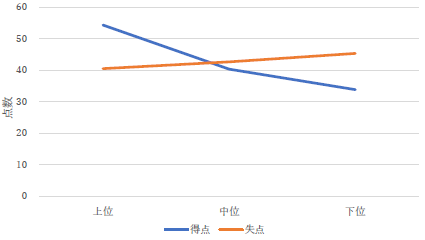
プロット点が無いですね.どこがデータがあるところなのかがわかりませんので,プロット点はこのようなケースでは必須です.線は無くても良いですが,プロット点が無ければ意味がありません. |
|
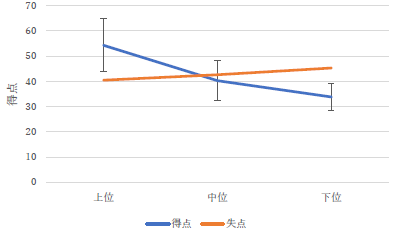
エラーバーが片方のデータにしか無いですね.どうしたんでしょうか? |
|
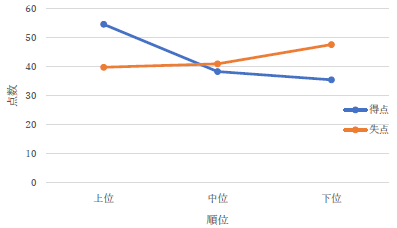
失点のデータが間違っているようです. |
|
交互作用の p 値の部分がなぜか抜けています. |

|
有効数字がどうにも気になりますね.0.999999... と続けるとそれだけ有効数字があるということになってしまいます. |

|
どうして左のような結論になるのでしょうか? |

|
要因AとかBとは,サンプルデータとして使用した例がAとかBだったからです.自分で実際に分散分析を行ったのだから,適切な表現に直して下さい. |
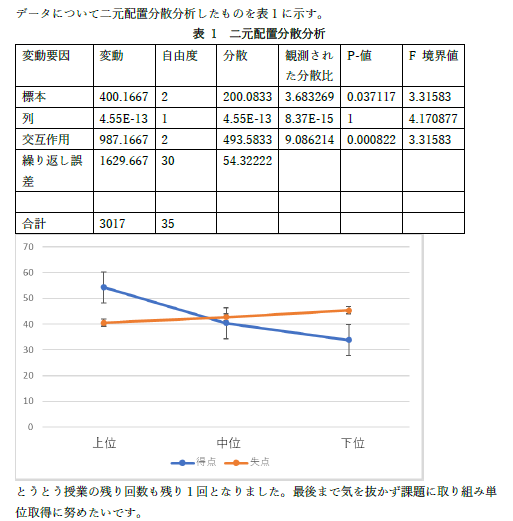
|
これが全てです.分散分析の結果も記述がないし,考察もないです.心意気は十分かもしれませんが,内容も十分に作ってください. |
二元配置分散分析について学習しました.分散分析表や結論の表現の部分がかなりややこしいので,前回のWebテキストをしっかり見なおして下さい.
資料を参考に予習してください.
χ 2 検定について学習します.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは翌週の火曜日の13:00までです.よろしくお願いします.
Back