• 前回の宿題について
  
• 前回の復習
  
• 自習資料
  
• 演習
  
• 次回の予習範囲
• 宿題
  

さて，今回の設問は問題作でしたね．やっかいかけてすみませんでした．どのように問題作なのか，まずはそれを見てみましょう．

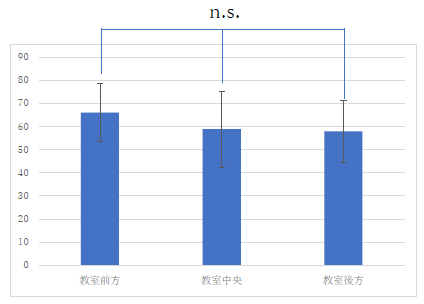
結果のグラフは以下の図1のようになりました．

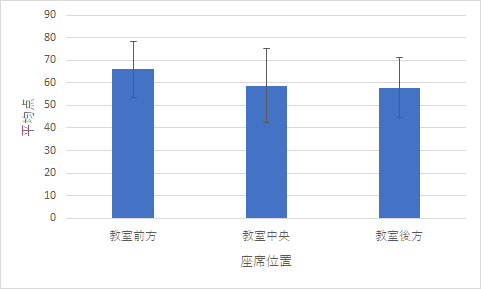
図1 結果のグラフ

一元配置分散分析をかけてみると，3つの平均値の間には有意な差があることがわかります．

F (2,114) = 3.68, p = .028

という結果になりますので，危険率 p が 5% 未満で有意な差ということになります．

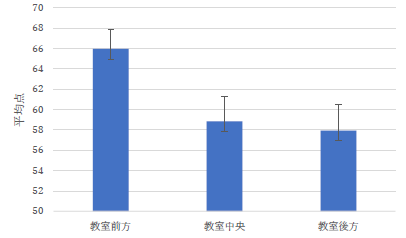
一方で，多重比較をテューキー法を用いて行うと，有意な差がある組み合わせを検出できません．分散分析と多重比較は別の作業なので，このような事例はちょくちょく起こるとされており，数%程度の割合で起こるようです．原因は，分析が仮定しているデータの分散が違うものであるのに，等分散として行うような場合が考えられます．そこで，今回のデータの度数分布を見てみます．（図2）

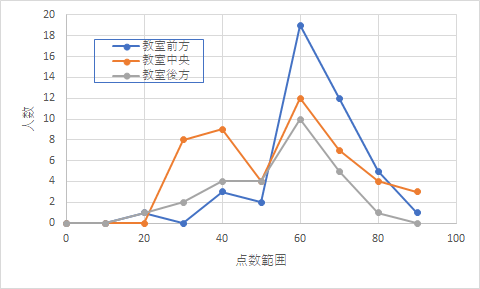
図2 成績分布

教室前方と後方は同じような分布ですが，教室中央がちょっと違う幅広い分布のようです．この程度の違いであれば，有意差が出てもよい気もしますが，今回は検出されませんでした．

ということで，じゃあ結論はどうなるのか，というと，まず分散分析によって有意差が確認されましたので，平均値の間には有意な差があることは確実です．一方で，どの平均値の間に差があるのかについての多重比較では有意差が検出できませんでしたので，具体的に記号で示したりすることはできません．

ということで，分散分析を行っているのに有意差がないという考察はちょっと不味いですね．そして，一番重要なのは，ネットなどにも書かれているのですが，成績が優秀な人が教室前方に座っているのではなく，教室前方に座っている人が良い成績を取る傾向にある，ということです．そこは間違えないで下さい．大きな教室で授業を受ける際には，前方に座れば成績が上がります．要因はいろいろですが，逆に後ろに座る人は何をしたいのかを考えてもらえばわかるでしょう．内職をしたい，スマホをいじっていたい，など，授業に向う意識の低い人，教員が話していることが特に聞こえなくても気にならない，黒板やスライド資料が見えなくても特に気にならない，という人が多く後方に座るということです．

参考のために3つのデータについて，それぞれ t 検定を行うと以下のような結果になり，2つの平均値間に有意な差が認められます．

表1 各データ対の t 検定の結果

データ対	前方ー中央	前方ー後方	中央ー後方
p	.024	.013	.804

さて，それではいつものようにグラフから気になる点を見ていきましょう．

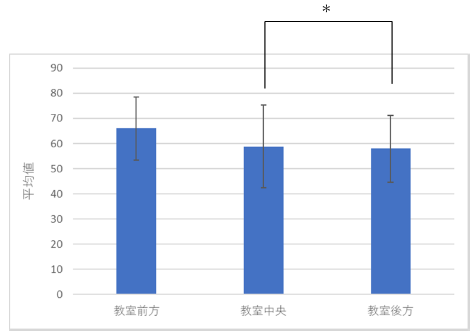
	上で説明したように，今回左のように明確に有意差を表示するような結果にはなりませんでした．
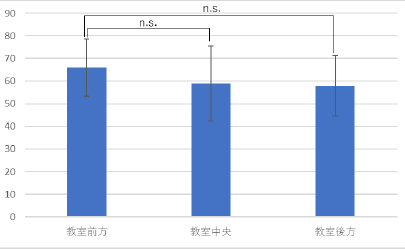
	分散分析の結果と合わせて考えると n.s. は付ける必要は無いと思いますが，つけるのなら全部の組み合わせに付ける必要があります．
	こういう分岐するような描き方はしないと前回も説明したはずですが．
	高さを比べるグラフで原点が無いのはダメだとずいぶん前に説明しています．

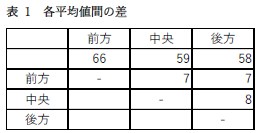
	平均値が整数になっているのはなんででしょうか？
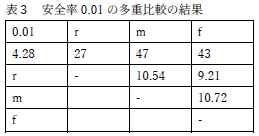
	記号 r m f の説明が文中にありませんし，量を表す名前で無いのであれば，アルファベット小文字1文字で表すようなことはあまりしませんが．また，安全率というのも聞いたことがありません．
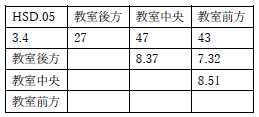
	臨界差の値が間違っています．
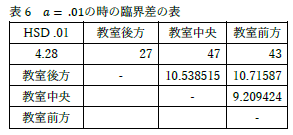
	今回多くの人がやっていたのが左の例のように α = .01 のときの臨界差の算出です．先に分散分析を行った人であれば，そこでの p が .028 であるので α = .05 だけで十分と判断できるはずです．また，多重比較のみを行うのであれば，まず α = .05 で計算し，そこで有意差が無いのであれば，α = .01 の場合を行う必要がありません．ただ何も考えずに作業としてだけやっていると，このような意味のない無駄なことをやってしまいます．

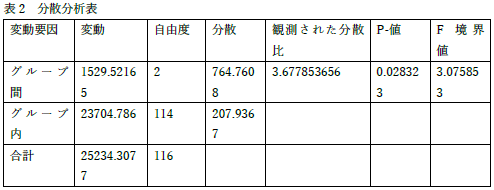
これまで何度か指摘しました．表の中の数値の改行はありえません！

最後は考察に関するものです．

p = .0283 なのになんで帰無仮説は棄却できないのでしょうか？忘却できるかどうかはさらに不明ですが．

分散分析をやっていれば有意な差があるという結論が一方では出ているのに，一刀両断ですか？

多重比較を行いました．分散分析と併用することで，どの平均値の間に有意な差があるかを見つけることができるものでした．データの解析の中で必要とする機会も多いので，きちんと理解しておきましょう．

資料を参考に予習してください．

1. 二元配置分散分析練習

   今回はEXCELでの制約のために，全ての群でデータの個数が同じ場合を扱います．より一般的な，繰り返しの数が異なる場合についても当然できるのですが，この授業ではとりあえず繰り返しの回数が同じものだけに限定して実習します．

   1. データの準備

      リンク先の資料を用いて練習を行います．まずは，準備してください．下図のようなデータがあらかじめ入っています．

      

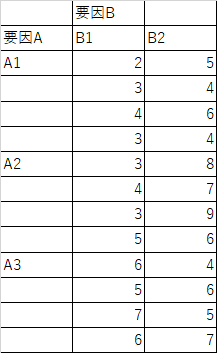
   2. ANOVA作業

      EXCELのワークシートの一番左上からデータが始まっているとします．A2からC14までのセルを選択して，「データ」メニューから「データ分析」をクリックして「分散分析：繰り返しのある2元配置」を選択して，分散分析を実行しましょう．今回自分で入力する必要があるのは，「1標本あたりの行数」と「出力オプション」だけです．行数は各条件で4行ずつとなっているので4を入力し，分散分析表の出力先は適当なセルを選択しておきましょう．

      出力される結果は以下のような表になるはずです．

      

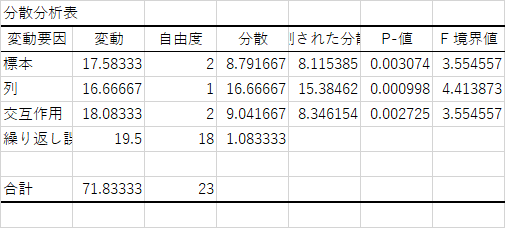
      EXCELが出力する分散分析表で，「標本」というのは今回で言えば要因のA1からA3の条件によるものが対応し，「列」がそのままの意味の列，すなわち，B1とB2の条件による違いのことです．

   3. 結論

      今回の二元配置分散分析の結論は以下のようにまとめられます．

      • 要因Aに主効果が見られた．(F₁₈² = 8.11, p = .0031 )

      • 要因Bに主効果が見られた．(F₁₈¹ = 15.38, p = .0010 )

      • 要因AとBに交互作用がある．(F₁₈² = 8.35, p = .0027 )

      グラフも一緒に見ながら考えてください．

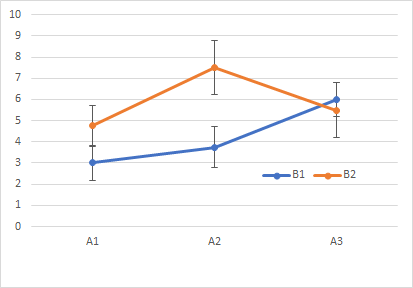
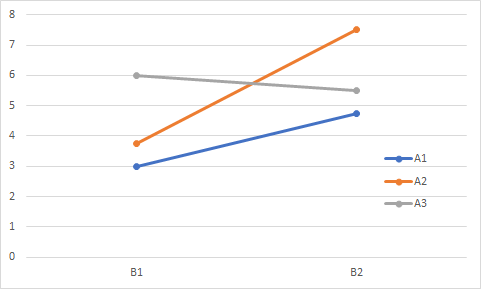
      二元配置分散分析の結果をグラフで表現するのに，上の2つの図のような表現が可能です．どちらを選択するかは，自分が強調したい結果がより分かりやすくなるのはどちらかで決まります．そのため，同じ表からどちらも作れるようになっておく練習もしましょう．

      以前に実際のグラフでは折れ線グラフは使用しないと言いましたが，二元配置分散分析の結果を分かりやすく表示するために使用することはありました．すみません．

2. 演習
   1. 資料にあるデータ

      リンク先の資料のデータについて，二元配置分散分析により平均値について議論してください．グラフの作成も行いましょう．

   2. 松江市の40年間の8月の気温

      リンク先のデータを使用して，1982年から2022年まで10年毎の8月の平均気温の推移を分析してみましょう．それぞれのデータは8月上旬，中旬，下旬（30日まで）に区切り，旬ごとの平均気温と観測年の二元配置としてください．グラフも作成しますが，ごちゃごちゃするので，エラーバーは無しとします．

   3. 冬の気温

      冬の気温の経年変化についても見てみましょう．リンク先のデータは松江市とほぼ同じ緯度にある海に面しているか，比較的海に近い都市の1月上旬，中旬，下旬の平均気温を2017年から2023年までまとめたものです．都市と観測年の二元配置分散分析をしてみましょう．こちらもエラーバー無しのグラフを作りましょう．

次回は χ ² 検定について学習します．予習用の資料を参考に予習してください．

いつものレポート提出システムを利用して行います．

宿題の公開は原則として水曜日の18:00からとなります．また，提出の締め切りはですが，来週は火曜日が水曜授業のため，採点に要する時間を考慮して14日金曜日の15:00に早めます．急な変更ですみませんが，ご理解よろしくお願いします．