- 本日の作業内容
- 1元配置分散分析
t 検定で実施した平均値の検定ですが,平均値の個数が3個以上になると分散分析で有意差について検討します.その際に,単純に平均値の個数が増えただけの状態が1元配置となります.学校のクラスの平均点などでは1組〜5組までを考える,というような場合がそれに相当します.このようなクラスの違いを「要因」と言い,5組まであるのなら「水準」が 5 というように言われます.一方,1 年生から 3 年生までのそれぞれ各クラスというようになると,要因が学年とクラスの2つになりますので,そのような場合は 2 元配置と呼びます.2元配置は後ほど行うことにして,今回は 1 元配置の分散分析について考えます.
- 準備
初めてWindowsで分散分析を行う場合にはエクセルに機能を追加する必要があります.以下の作業を行ってください.
Excelでは統計分析を行う環境はデフォルトでは見えないようになっていて,「アドイン」で追加する必要がありますので,まずはその準備から行いましょう.
- アドイン追加作業
まずは,「ファイル」メニューを開いてください.すると,図1のように一番下の方に「オプション」がありますので,それをクリックします.
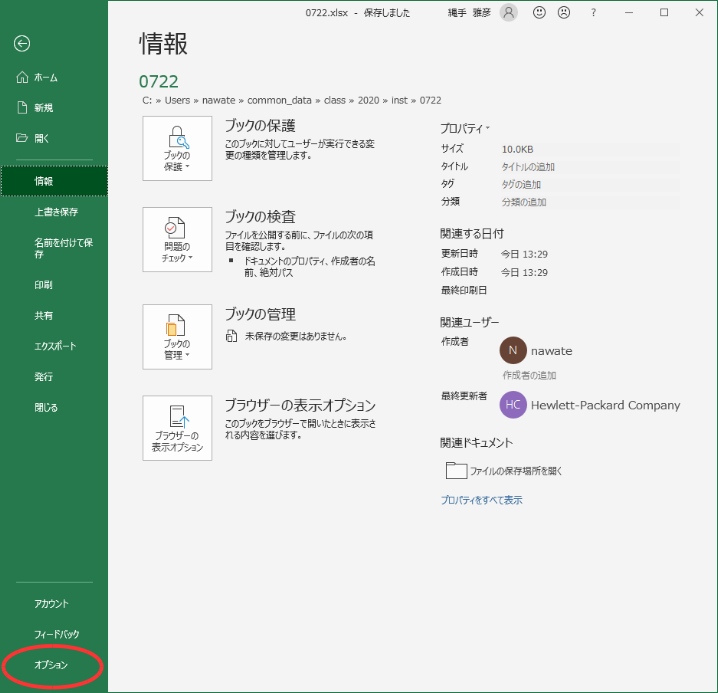
図1 「ファイル」ウインドウ「オプション」をクリックして開いた図2のウインドウの中の「アドイン」をクリックします.
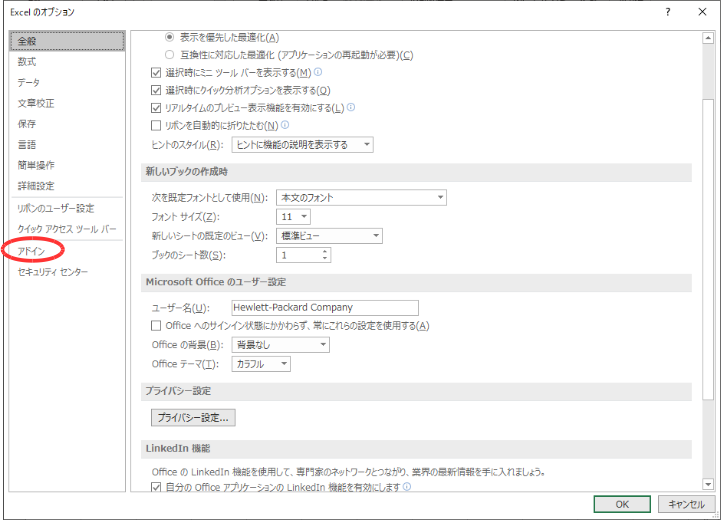
図2 「オプション」ウインドウ図3のウインドウが表示されるので,「アドイン」の中から「分析ツール」をクリックして選択し,「設定」ボタンをクリックして下さい.
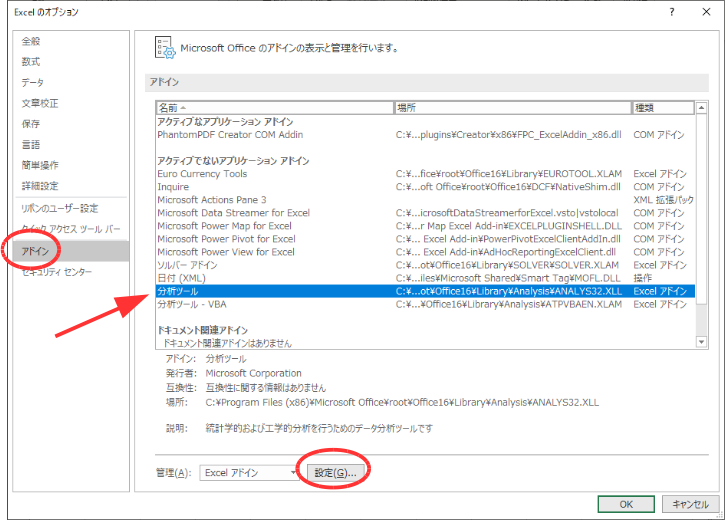
図3 「アドイン」選択ウインドウ図4のウインドウが表示されるので,「分析ツール」のチェックボックスにチェックを入れて「OK」ボタンをクリックします.
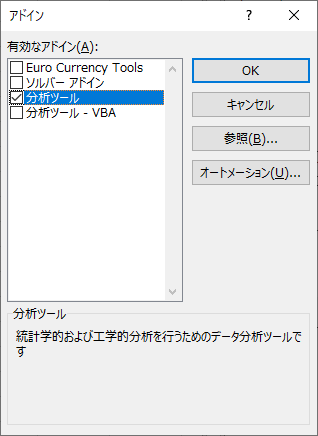
図4 分析ツールの選択ホーム画面でファイルメニューから「データ」を選択すると,図5のように「分析ツール」が追加されていることが確認できるはずです.
図5 「データ」タブへの「分析ツール」追加
- アドイン追加作業
- 実際の検定作業
最近の表計算ソフトでは分散分析はあらかじめ用意されていますが,単純に関数一つでできるようなものでも無いので,メニューから呼び出して使用する形式になっています.以下の例で試してみましょう.
- データ
使用するデータはリンク先のものとします.このデータには水準がA〜Dの4つあります.以下の手順で分析してみましょう.
Excelのデータメニューにある「分析ツール」をクリックすると図6の画面が表示されるので,「分析ツール」の先頭にある「分散分析:一元配置」を選択して「OK」をクリックします.
図6 分析ツールの選択図7の画面に変わるので,入力範囲を設定してください.見出しの部分も含めて選択し,「先頭行をラベルとして使用」にチェックを入れておくと,項目名として自動的に入れてくれるので助かります.α の値はとりあえずデフォルトの 0.05 のままで構わないでしょう.
出力先はデータと同じ表の中に出す場合には「出力先」を選択して,自分で場所を入力します.↑ボタンで設定します.別のシートに出す場合には「新規ワークシート」で,別のファイルとする場合には「新規ブック」になります.
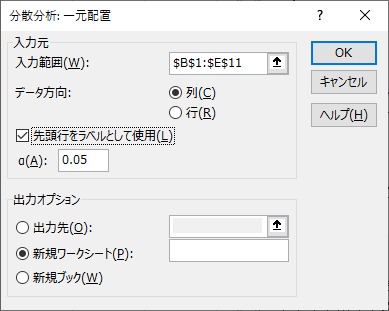
図7 分散分析の設定画面設定が完了して「OK」をクリックすると結果を図8のように表示してくれます.分散分析表も出してくれますし,危険率 p の値や,p が0.05となる F の値も計算してくれています.
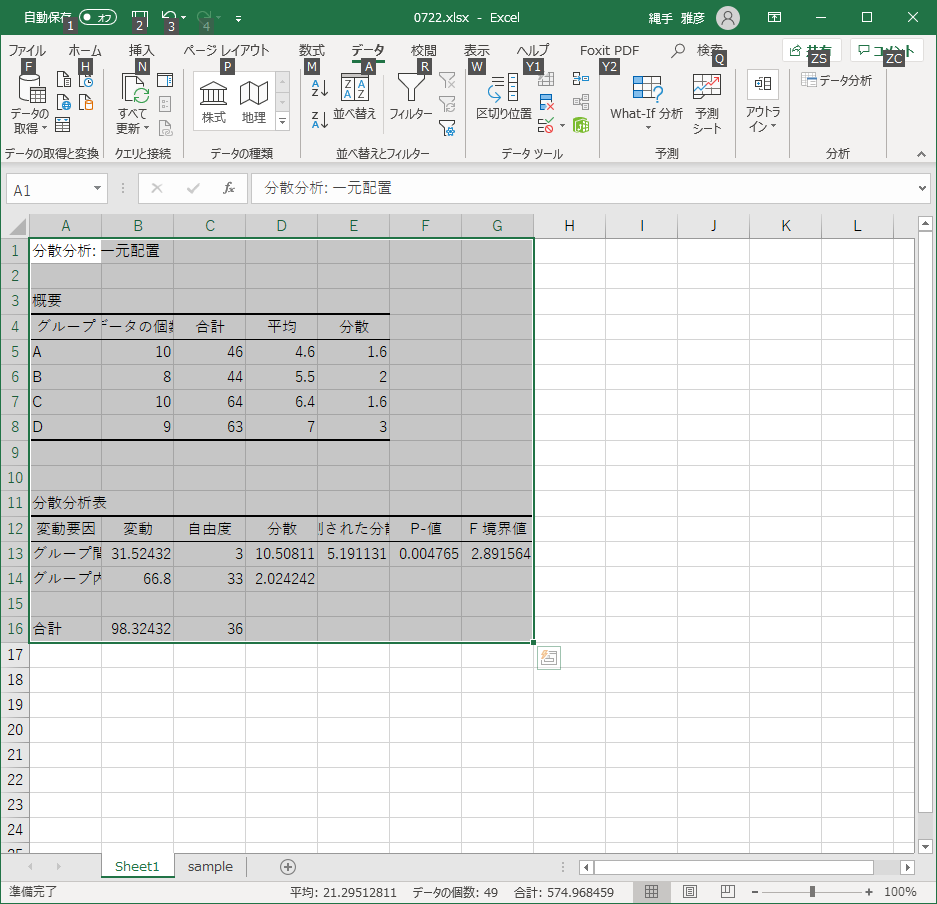
- 分析
分散分析表には簡単な説明もついていますし,資料の方にも載せているのでそれを参考に見ていきましょう.まずは,各グループの平均と分散が計算されています.続いて下に分散分析表が来ます.
群間の変動と群内の変動,自由度,残差の平方和( SB と SW ),それらの比( F 値),そしてその F に対応する危険率 p ,最後が p =.05になる F の値という順番です.
- 検定結果
この例題の検定結果は以下のように記述します.
群A〜Dに関して以下の平均値が得られた. m A = 4.6, m B = 5.5, m C = 6.4, m D = 7.0 帰無仮説: これらの平均値の間には有意な差はない 検定結果: F (3,33) = 5.19, p = .0048 よって,帰無仮説は棄却可能 これらの平均値の間には有意な差がある
ただし,分散分析単体ではどの平均値の間に有意な差があるかはわかりません.それについては次週の多重比較で扱います.
- データ
- その他のデータによる作業
以下に示すデータについて,エラーバー付きのグラフを作成した上で,それぞれ一元配置分散分析を行いましょう.
- J1リーグチームの得点と失点
昨年度のJ1リーグのシーズンを通しての得失点のデータを用意しました.上位6チーム,中位6チーム,そして下位6チームの得失点について分散分析によって特徴を見てみましょう.
- コロナ死者数の地域差
2023年5月8日で新型コロナウイルスが5類になってしまったので,現在の感染状況は分からなくなってきましたが,それ以前の各都道府県のコロナ死者数のデータを使って,北海道・東北,関東,中部,近畿,中国,四国,九州・沖縄の7地域での状況を考えてみましょう.
- 産業データ
前回の宿題で使用した都道府県別の製造品出荷額,農業産出額について,上と同じように7つの地域に分けて分析してみましょう.
- J1リーグチームの得点と失点
- 次回の予習範囲
今回は日本国内の人口動態や地理的条件などについて関係しそうないくつかの統計指標との相関について考察してもらいました.もちろん他にも細かい統計量は無数にありますが,今回はほんの一端を覗いた程度でした.
さて,まず人口との関係について見てみると,以下の関係が見つかりました.
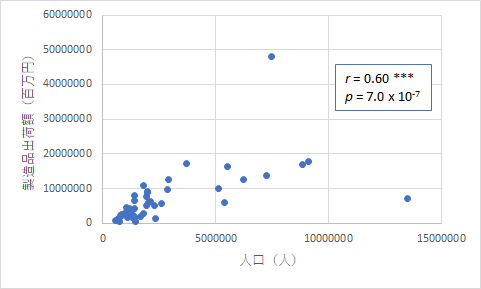
上の図を見ると,人口が多い都道府県ほど工業製品の出荷額が多くなるということです.東京都と愛知県という外れ値とも呼べるような極端な値もありますが,無相関検定の危険率は p = 7.0 × 10-7 ということですので,かなりの相関がありました.
データを加工してから見比べることをしてみると以下のような関係も見つかります.
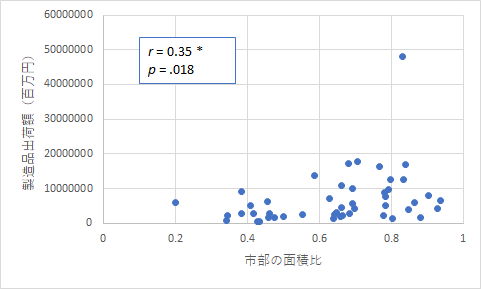
上の図は都道府県の面積に占める市部の比率に対する製品出荷額の図です.そうすると,有意な相関があることがわかります.単純な面積では見つからない相関も,ちょっとの加工で見つけることが可能です.ここでもやはり愛知県が外れ値になってしまいますね.
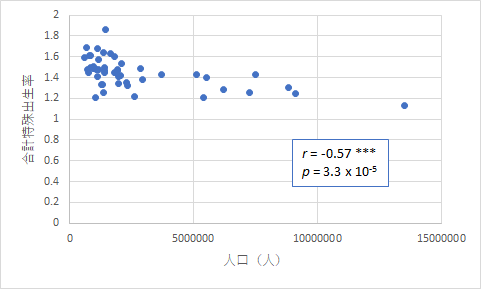
一方で,上のような関係もありました.人口が多い都道府県ほど出生率が低いということで,こちらも強い相関と呼べるものでしょう.大都市圏は地方から若者を吸い上げる割には子供が増えないということで,現在の日本の問題が端的に現れているようです.特に若い女性の流出が増えているという指摘もありますが,地方の古臭い男尊女卑や伝統的価値観という名の女性の無償労働が必須の状況が変わらない限り,この傾向は続くのでしょう.
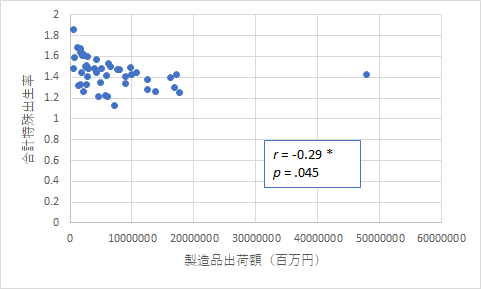
また,上の図のように工業製品の出荷額の多い都道府県ほど出生率が低いという結果も出ました.大都市圏での出生率が低いことが関係しているのでしょう.この相関係数から人口の影響を取り除いた偏相関係数は r = 0.073 になりますので,やはり都市圏の人口の問題のようです.
今度は農業の観点で見てみましょう.農業製品の生産額は面積と関係していることは容易に推測できますが,市部と郡部の面積はどう関係しているでしょうか.
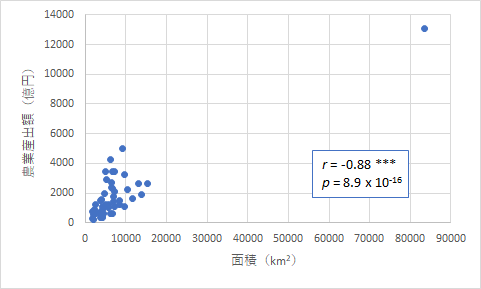
|
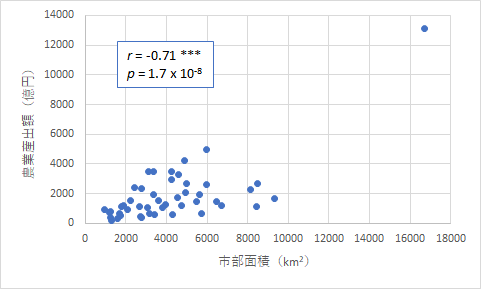
|
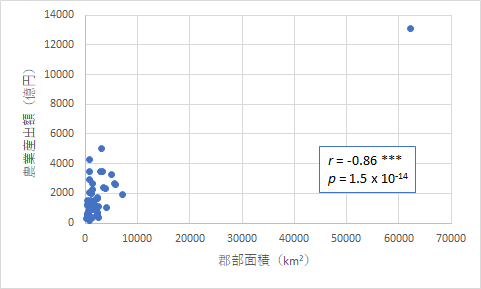
|
上のようにいずれも危険率が非常に小さい値となり,有意な相関であることはわかります.ただ,グラフを見ると,どう見ても北海道が強く影響していることがわかります.そこで,念の為,北海道を除去したものも作ってみました.
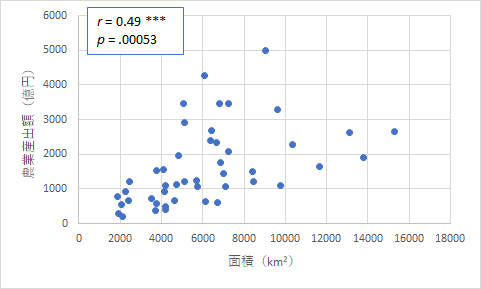
|
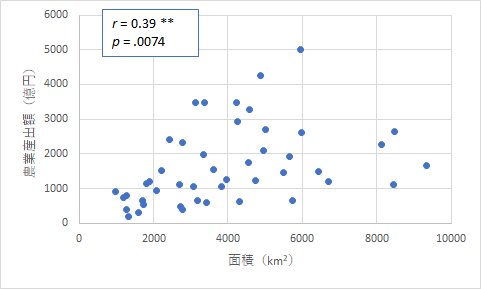
|
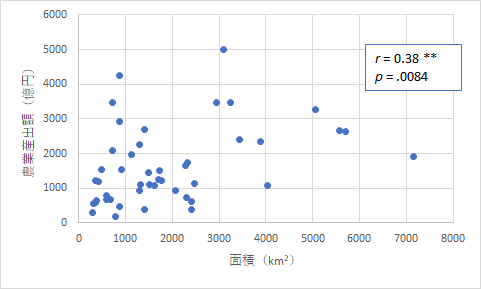
|
これらを見るとやはり有意な相関ではありますが,ばらつき具合がよく見えるようになりました.また,郡部の面積というのは特に影響しないということも言えそうです.
さて,皆さんから出してもらったレポートですが,ちょっと残念だったのは,設問のところに書いていた「関係しそうな組み合わせについて散布図を作りましょう.」という表現で,自分の思い込みで,少ししか散布図を用意しなかった人が結構いたことです.数値の表を見ただけで,相関が読み取れる特殊な能力が無い限り,まずは散布図をざっと眺めて,相関がありそうなものについて,きちんと軸の説明を入れたり,考察を進めたりする必要がありますが,どうだったでしょうか?
わざわざ合計特殊出生率なんて入れるんだから,絶対関係あるでしょ?とか思いませんかねえ.1つの散布図しか作らず,また自分はそれしか相関がある組み合わせは無いと思った,という人は社会に関する知識や興味があまりに不足しているということです.もっと社会をよく知りましょう.
以下は例によって残念な例の一部です.参考にしてください.まずは,グラフに関するものから見ていきましょう.
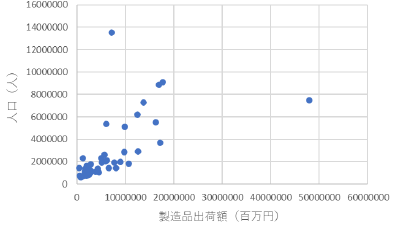
|
工業生産による所得が人口を支えるということも無いでは無いでしょうが,通常の観点からいうと,縦軸が人口というのは適切ではありません.横軸の変数(独立変数)が縦軸の変数(従属変数)に影響を与えると考えるのがグラフの基本です. |
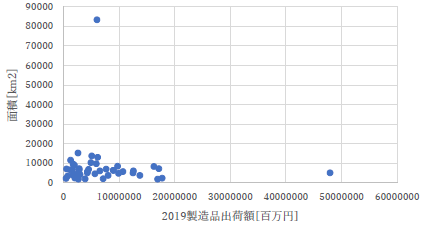
|
こちらも同じく縦軸が面積というのがどうにもピンときません.工業生産が活発になると面積が増えるという仮説でしょうか?確かに港湾部であれば埋め立てを行うというようなことがかつてはありましたが.それと面積の単位が km2 となっています.ちゃんと上付きの km2 で表現してください. |
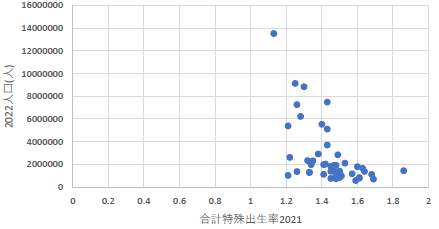
|
これもで,横軸が合計特殊出生率というのにちょっと疑問が残ります.出生率が高いほど人口が多いと言う仮説は無いことも無いですが,昨今の事情からすると,出生率に影響を与える因子が何か,を探ることが少子化対策としては必要です. |
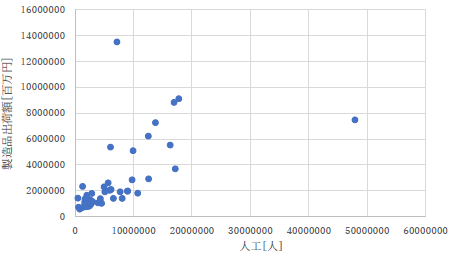
|
ありがちなタイプミスですが,この人のレポートのグラフは全てこの「人工」になっていました.ちゃんと見直しましょう. |
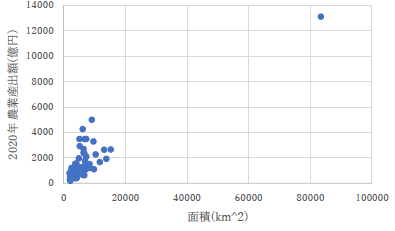
|
こちらもこれまで何度も指摘した不適切な上付き表現です.もし知らないのなら,参考までに書いておきますが,EXCEL ではテキスト中の上付きや下付きにしたい部分を選択して右クリックで出て来るコンテキストメニューの「フォント」を選択すると,文字の修飾が出来ますので,以後はちゃんと使ってください.ときどき「スペルチェック」機能が働いてメニューが見えない場合がありますが,その際には「すべて無視」を選択して,もう一度右クリックするとフォントメニューが出てきます. |
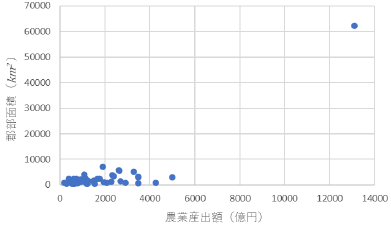
|
これも何度か指摘しましたが,単位はイタリック(斜体)にはなりません. |
以下は表現や考察に関するものです.

|
先週の Web テキストに書いたのは「もしくは」ということで,どちらかを選んでくださいという意味です.実際に危険率 p の値が得られるのなら,不等号の方は不要です.次回行う予定の多重比較では p の値は求まりませんので,不等号の表現の方を使用します. |
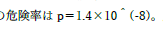 こちらの上付き表現も何度もダメだと指摘しました.いい加減やめてください.
こちらの上付き表現も何度もダメだと指摘しました.いい加減やめてください.
|
|

|
相関係数は負の値になったはずですが?ちゃんとグラフを作りましたか? |
なお,散布図などのグラフを作成する際の x 軸の量と y 軸の量の入れ替えですが,万が一知らないために,上述のような適切でないグラフを作成していたとしたら問題ですので,一応やり方を説明したページを作りました.参考にしてください.
前回は無相関検定でした.有意な相関かどうかを見るものでしたが,検定の場合はまとめの表現が難しいので,早いところで慣れておくようにしましょう.
資料を参考に予習してください.
2つの平均値の間に有意な差があるかどうかは t 検定により確認できましたが,平均値の個数が3つ以上になると, t 検定では確認できません.そこで分散分析を行うことになります.今回は分散分析について実習します.
次回は多重比較について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは授業翌週の火曜日の13:00までです.よろしくお願いします.
Back