- 本日の作業内容
- データの例
- t0 の計算
次に示す2つのデータについて,資料の式(1)から t0 の値を求めてみましょう.
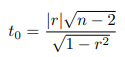
・・・ (1) データ番号 x y 1 2 12 2 5 5 3 6 18 4 9 19 5 12 4 6 14 8 7 15 11 8 19 26 9 25 29 10 27 12 11 28 21 12 31 16 13 34 28 14 36 17 データ番号 x y 1 3 10 2 5 15 3 6 17 4 9 11 5 12 18 6 15 19 7 16 28 8 17 16 9 19 24 10 24 26 11 26 19 12 29 31 13 31 25 14 33 39 15 34 27 16 38 40 17 40 29 18 41 38 19 43 44 20 48 32 21 52 46 無相関検定を行う場合の自由度は t 検定のときとは異り,データの組の数を基準にします.自由度は n - 2 なので,上の場合ではデータの組の数から2を引いて12,下の表では19ですね.
- p 値の算出
得られた t0 の値に対して, t.dist() 関数により p 値を求めて,検定を行ってください.
t.dist()の引数仕様はMicrosoft365版では,t 分布の横軸の値 x,自由度,関数形式,となっています.ポイントは最後の関数形式の部分で,TRUEを指定すると累積確率を返してくれます.ということは,全確率である1からその値を引くと,それ以外の領域の確率を出してくれます.その意味がわかりづらいのですが,別途両側確率を返してくれるt.dist.2t()という関数で確認するとわかりやすいかもしれません.t.dist.2t()関数の引数仕様は,x,自由度,だけとなっていますので,単純に両側確率を返すだけです.
t 検定では,二つの値を比較して,「一方がもう一方よりも大きか」だけを検定する「片側検定」と,「二つの値が異なるか」を見る「両側検定」の2つがあり,今回は異なるかをみる両側検定を使用しますので,上の説明のようにして t0 から危険率 p が求められます.
古い関数であるtdist()を使うと,引数使用が,x,自由度,分布の指定,となっており,分布の指定では「1-片側検定」「2-両側検定」となっていて分かり易いかもしれません.無相関検定で使用する関数比較 関数 引数仕様 使用法 t.dist() x,自由度,関数形式 2 * (1 - t.dist()) の値が両側検定の p に対応 t.dist.2t() x,自由度 自動的に両側検定の p に対応 tdist() x,自由度,分布の指定 「分布の指定」を2として両側検定にの p に対応 - 検定の表現
以前にも説明しましたが,現状検定について学習している状況ですので,検定結果をまとめる際にはしっかり正確な記述を心がけましょう.
帰無仮説:量○○と●●の間には相関は無い 検定結果: 危険率 p < .05 もしくは p = .0** (Φ = **) 帰無仮説を棄却可能 量○○と●●の間には有意な相関がある 危険率 p ≧ .05 もしくは p = .1** (Φ = **) 帰無仮説を棄却できない 量○○と●●の間には有意な相関は無い 注)*は任意の1文字(数字)
- t0 の計算
- 検定実習
- 先週のデータ
先週の演習で使用したデータを使用して,有意な相関であるか,無相関検定で確認してみましょう.
気温の推移
ジェンダーギャップと出生率
ジェンダーギャップと出生率(民主主義国)また,宿題で使用したJリーグとWEリーグの順位相関
- 子育ての男女時間比率
内閣府の男女共同参画白書のデータを使用して,夫婦の子育てに関わる時間と出生率の相関について検定を行ってみましょう.
- 先週のデータ
- 次回の予習範囲
今回は日本のプロサッカーリーグの代表であるJ1リーグと発足してまだ2年しか立っていないWEリーグの2シーズンの順位相関をそれぞれ見てみました.作業自体は単純なので,だいたい出来は良かったようです.
まず,結果としてグラフにすると次のようになります.
|
|
|
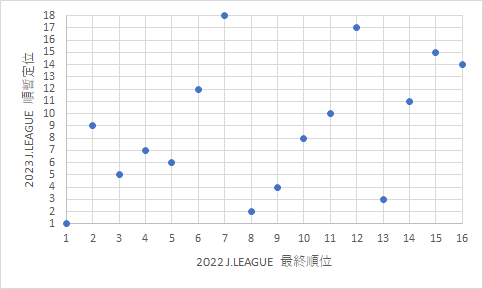
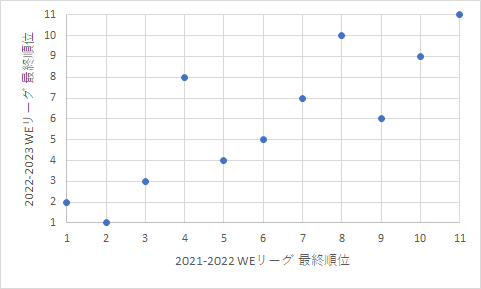
| 図1 J1リーグ | 図2 WEリーグ |
細かいことを言うと存在しない順位を縦軸や横軸の目盛に表示させる必要は無いので,上の図のようになりますが,今回は傾向を見るだけの図なので,目盛については特に減点などの対象にはしませんでした.
では,相関係数ですが,Excel 標準の correl() を使用して一発で求められます.値はJ1リーグが 0.45 で,WEリーグが 0.85 でした.どちらも相関があると言えますが,値には大きな違いがあります.
考察では多くの人が様々な意見を書いてくれていました.皆さんからの指摘のようにJ1リーグは,現在J3まであるサッカーリーグの頂点であり,毎年入れ替え戦などを行うトップリーグです.資金力のあるチームも多く,選手の補強も積極的で,前年度の成績が悪い場合には様々な対策を行うため,戦力の均衡がある程度までは保たれています.しかし,それでも強いチームは強いので,相関があるにはあります.最強チーム3年説というのもあり,能力の高い選手は海外に移籍したり,また,能力が高いにもかかわらず先発起用がすくない選手は出場機会を求めて他チームに移籍したり,さらには戦術が相手チームに研究されるなど,だいたい数年で強いチームも入れ替わります.
一方で,WEリーグは選手層が薄く,観客数が少ないこともあり,資金力が十分なチームはほとんどありません.そのため,多額の資金で有力選手を引き抜くこともできない状態で,発足時の戦力不均衡がまだまだ続きそうです.
さて,皆さんから出してもらったもので,例によって気になるものを以下に挙げます.参考にしてください.
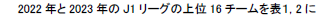
| 2022年の1-16位のチームも今年は1-18位に散けるので,16チーム限定ということはありません. |
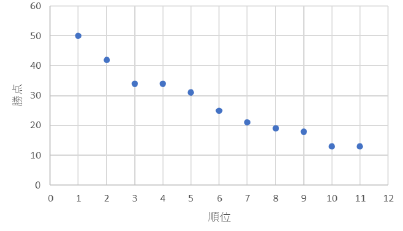
| なぜこのようなグラフに?勝ち点で順位を決める規則なので,順位と勝ち点が相関するのは当たり前です. | |
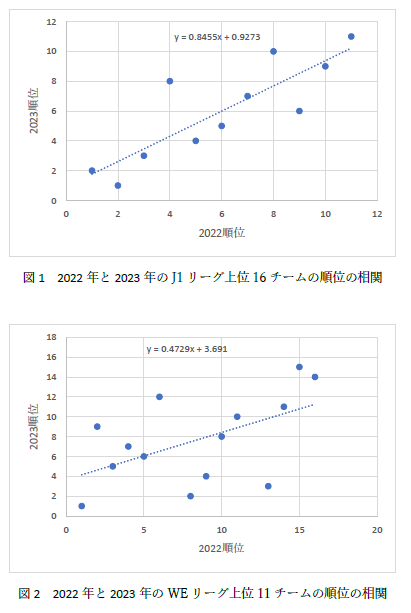
| キャプションとグラフが一致していませんし,相関を見ているので,回帰直線には意味はありません. | |
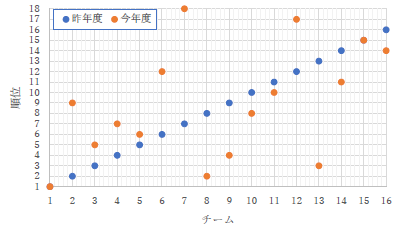
| 昨年度の順位を横軸に,昨年度の順位をプロットすると当然 y = x の直線になりますが,そのプロットに意味はありますか? |
次に示すのは,これまでの何度か見られたのですが,そろそろ指摘しておかないと今後も続きそうなので,今回はお見せします.

| 図のキャプションが図と違うページに行ってしまっています.それはよくありません. | |

| 左の例は表が途中で切れて別ページに一部が表示されているものです.これもよくありません. |
後はだいたいいつものように気になるものです.
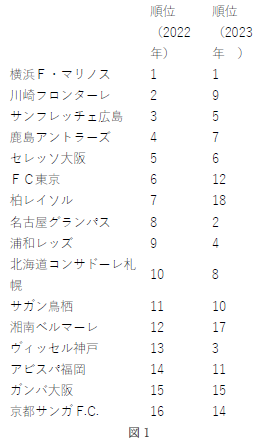
| 左のこれは「図」ですか? | |
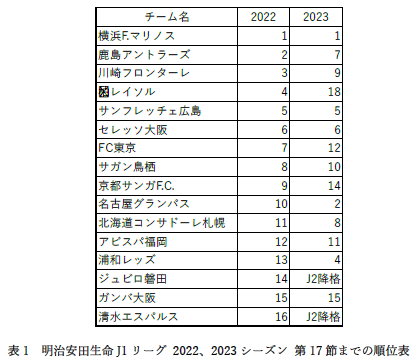
| 表のキャプションは「表の上」につけます. |
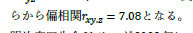
|
偏相関係数も相関係数の1種ですから,値は -1 から 1 の範囲しか取りえません. | |
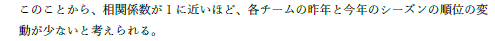
| それって当たり前ではないですか?考察ですか? | |
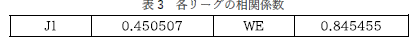
| 有効数字が守られないケースはなかなか無くなりません. | |
| 以前にも指摘しましたが,日本語の文章中で使用する句読点は,日本語フォントの「,」や「.」を使用するか,半角文字コードを使用するなら,スペースを続けて入れて,空白を確保してください. | |
相関係数について実習しました.あらかじめ用意されている関数 correl() を使用することで,相関係数を求めることができました.ところで相関係数の大きさで相関の強さを表現することが一般的に行われていますが,実際に有意かどうかは今回の検定の結果を見てみないとわかりません.
資料を参考に予習してください.
無相関検定を行います.一般的な表計算ソフトには無相関検定の関数は用意されていません.そこで,以下の流れにそって簡単な作業をいくつか行います.
前回相関係数について学習しました.相関係数 r の絶対値が1に近いほど強い相関があり,0に近い場合には相関が無いと一般には言います.しかし,相関が有意なものかは相関係数の大きさだけでは判断できない場合があります.データの組が少ない場合などです.そのときに,相関係数の大きさから t 分布における t 値に直したものを利用して検定を行うことを無相関検定と言います.次からの例題で試してみましょう.
次回は分散分析について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは翌週の火曜日の13:00までです.よろしくお願いします.
Back