- 本日の作業内容
- 手計算による相関係数の算出
資料の式(2)に基づいて相関係数を計算してみましょう.以下の2種類のデータの組で計算します.
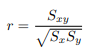
・・・ (2) データその1
x y 1 3 10 2 8 9 3 10 13 4 11 27 5 15 24 6 19 28 7 22 45 8 24 32 9 27 36 10 33 51 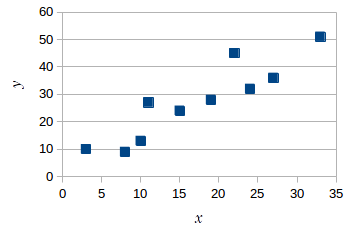
データその2
x y 1 3 106 2 8 110 3 10 80 4 11 76 5 15 102 6 19 98 7 22 79 8 24 65 9 27 88 10 33 92 11 39 96 12 41 67 13 42 88 14 46 92 15 55 57 16 58 59 17 69 65 18 74 81 19 77 43 20 81 53 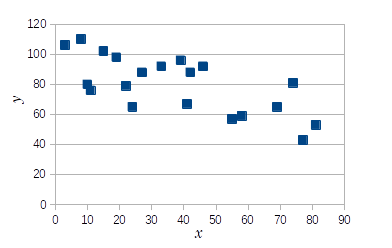
残差平方和を求める関数は devsq() でしたね.この関数を使用すると S x と S y はすぐ求められますが, S xy はまず xi × yi のデータを用意しないといけません.
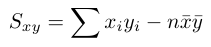
- 相関係数を求める関数
表計算ソフトには通常相関係数を求める関数が2つあり,名前は違うのですが,全く同じことを行うものとなっています.名前は一つは correl() で,もう一方は pearson() です.相関のことを英語で correlation というので,前者はその名前の短縮形,相関係数(正確にはPearsonの積率相関)を算出したのが Pearson という名前の人なので,後者はその名前が関数名になっています.動作は同じです.
先ほどの手計算による r = S xy / √S x S y があっていたかどうか,上記の関数を用いて確認してみましょう.
- 順位相関
上で説明している相関係数はデータが正規分布に従っているという前提で求めるものです.一方で,正規分布では無いデータを扱うノンパラメトリックな手法もあり,代表的なものがスピアマンの順位相関です.順位は整数値で表されるので,見かけ上の式はピアソンの積率相関とは違っているのですが,実際の計算は同じ結果になります.Excel では同じ関数 correl() で計算できます.
- 偏相関
授業資料にあるように見かけ上相関があるように見えるものの,その背景には別のデータが隠れていることもあります.そのような場合に,求めるのが偏相関です.資料の式 (4) で求められます.
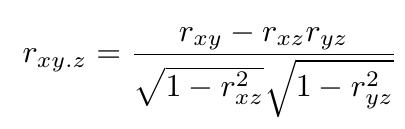
・・・ (4) たまに偏相関の事例として挙げられているものに,小学生の 50 m 走のタイムがあります.学年が上がるとともに平均タイムは短くなりますが,体格も変化しているので,データの見せ方としては体重が多いほど 50 m 走のタイムが速くなるように作ることもできます.しかし,その裏側には年齢も身長も筋力もあるので,何が相関に関与しているのか,きちんと見ないといけません.
- 演習
- 気温の推移
上の宿題の解説のところでも言及しましたが,気温は年ごとの変動も大きいので,長期的な視点で検討する必要があります.そこで,記録が残っている1941年から2022年までの年平均気温を松江市の場合で見てみましょう.
宿題で使用したサイトからのデータをまとめたものがありますので,グラフと相関係数で変化を見てみましょう.また,このままの気候対策だと回帰直線を求めることで将来の気温も予測できそうです.心配になりますね.
- 少子化
少子化問題が日本では深刻です.少子化の原因は複数あり多岐にわたっていますが,ここではジェンダー問題との関係について,相関係数から考察してみましょう.以下のデータを使用して作業します.
- ジェンダーギャップ指数と合計特殊出生率
世界各国の現状を確認するために,以下のデータを使用して,相関係数の練習をします.
合計特殊出生率(2020)とジェンダーギャップ指数(2022)
まずは単純に相関係数を見てみましょう.
- 政治体制の影響
いわゆる民主主義国家と分類しても良いと思われるヨーロッパ,北米,東アジアの国を抜き出してまとめたデータを使って,相関係数を見てみましょう.
- ジェンダーギャップ指数と合計特殊出生率
- 偏相関
- 気温の推移
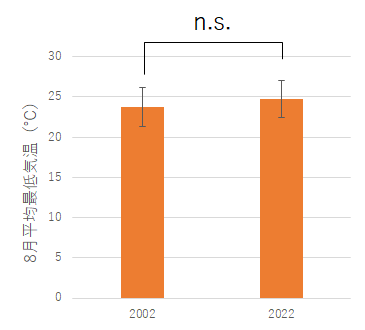
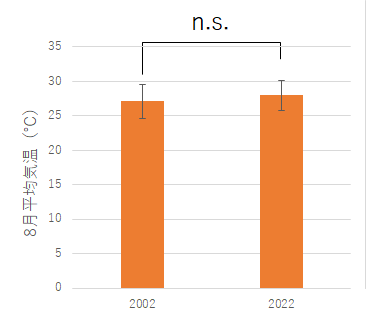
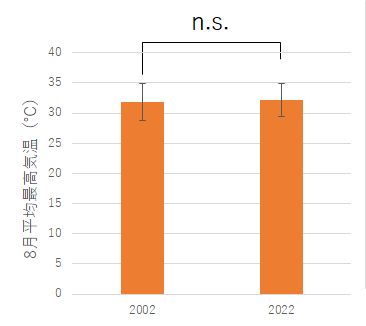
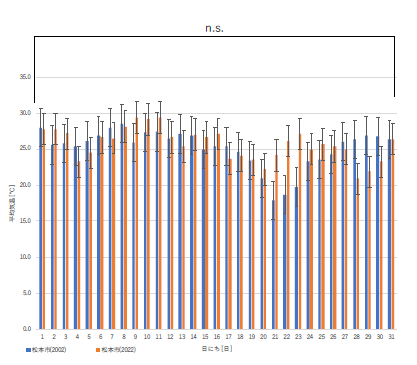
今回は課題として「平均気温」とだけ指定したので,気温のうちのどれを扱うのか,疑問に思う人もいたようです.地球温暖化の観点からは最高気温が気になるところですが,平均気温でも最低気温でも特に問題はありません.因みに,かなりの人が使用した2003年の松江市の気温ではなく,その1年前の2002年の松江市の気温で見ると,以下のような図となります.
|
|
|
||
| 最低気温 | 平均気温 | 最高気温 |
いずれの温度で比較しても2022年は2002年よりも温度は上昇しているものの,有意な差とまではいっていません.それぞれ危険率は,.11, .15 そして .60 です.
今回の作業は2つの年度を比較しているだけなので,実は温暖化の「傾向」をこれで見ることはできません.翌年2003年は2022年と有意な差が生じていますので,たった2つの年の比較ではしっかりした考察はできないということです.ただ,それでも有意な差が無いために温暖化が観測されていないという結論はだせません.それ以前と比べると明らかに有意に温度上昇をしています.例えば,1990年代前半以前の年と比較するとほぼ間違いなく有意な差が出ます.ちょうど皆さんが生まれたころにはすでに温度は結構上がっていて,昨年との差は地域によって出たり出なかったりという状況だったようです.
最小2乗法が終わって全体的に出来はよくなって来てはいますが,残念ながら仮説検定ならではの問題なども出てきており,要改善なものが多数ありました.以下にお示ししますので,参考にしてください.また,計測地を書いていないレポートが結構たくさんありました.こちらで確認できないので,やはりそこは記載してもらわないと困ります.
|
まったく意味がわかりませんね.t 検定というのは2つの平均値の間に有意な差があるかどうかを見るものです.平均値は2つです. |
|
エラーバーがおかしいです.誤差範囲からユーザー定義で実際の標準偏差を選ばずに,2つの平均値の標準偏差をつけるとこうなるはずです.ということで,やり方が間違っています. |
|
有意差についての記号がありません.グラフに記号が無い人も結構たくさんいました.きちんと指示していたので,そこはしっかりやってください. |
|
なぜ,テキストボックスと棒が重なります? |
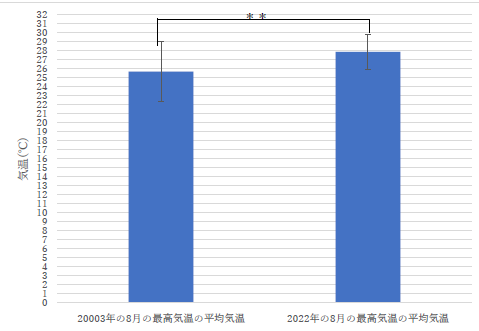
|
縦軸の目盛は0から32までの全ての数値が必要ですか?見辛く無いですか? |
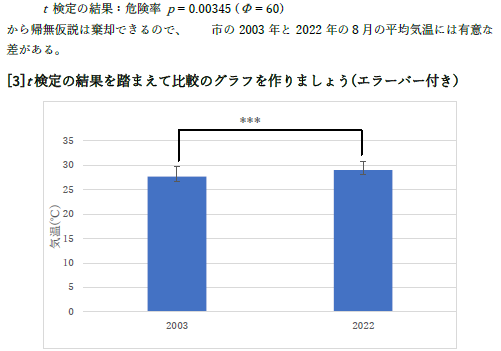
|
自分で計算しているように危険率は .003 ですので,.001 未満では無いですよね? |
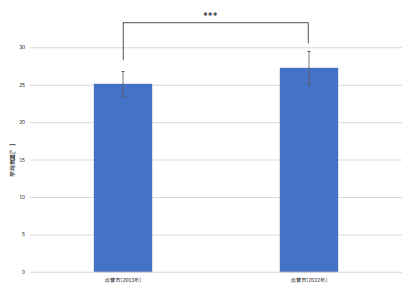
|
文字が小さくて見えません.フォントのサイズもちゃんと意識してください. |
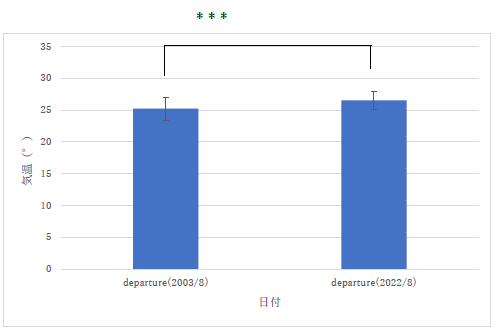
|
departure って出発という意味ですが,それがここで何か意味がありますか? |
次に,説明や検定などに関するものです.

|
有効数字について何も考えていませんよね.でも,レポート内のチェックリストではチェックが入っていました.何をチェックしましたか? |
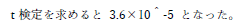
|
「t 検定を求める」とは? また,べき乗については上付きの指示を何度かしていますが,まだ改善されていませんね. |

|
今回何件か見られました.Webテキストにも予習用の資料にも検定をどのように行うのか,しっかり記載していました.まず,帰無仮説を立てて,それを棄却可能かどうか,危険率を見て判断します.それをきちんと書いてください. |

|
関数 ttest() が返している値は t 値ではなく,p です. |
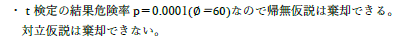
|
危険率が .05 未満となると帰無仮説を棄却可能となりますが,対立仮説を棄却できないということは何も証明していません. |
で,最後にときどき気になるものが出てくるのでそれについてちょっと.以下のものは,見づらいかもしれませんが,[2]の右側にうっすらと青い領域があります.これはなにかと言うと,Webページのテキストを選択してコピーし,Wordなどにそのままペースト(貼り付け)したことで,背景画像ごとペーストされてしまったものです.

このように不要なものまでペーストされるのを防ぐためには,ペーストしたい位置で右クリックして出て来るコンテクストメニュー
の「貼り付けのオプション:」の一番右の文字だけをペーストする機能を使って下さい.
統計的仮説検定の第一歩である t 検定について実習しました.表現が難しいので,上の例も参考にこれからはきちんと書くようにしてください.来週の作業で再び検定(無相関検定)がありますので,また使用します.
資料を参考に予習してください.
今回の内容は相関係数です.前々回まで最小二乗法を用いた回帰曲線について実習しましたが,似ているようで非なるものです.というのも,回帰という場合には理論的な背景から数式がある程度定まっていて,係数やべき乗などの検討を行う作業になるのに対して,相関は関係があるかないか,あるとしたらどのような依存関係にあるのか,を見るだけです.
例えば,夏の気温とアイスクリームの売上やビールの消費量の関係が有名なものです.これらは商売に直結するので,予想気温に従って仕入れやメニューを変更することで,顧客の需要を満たすことができます.そのため,その関係式はリサーチ会社から販売されるほどです.
で,ここで確認ですが,当然ですが夏の気温が物理的に何か作用してアイスクリームの売上に影響するのではありません.気温に従って人体の発汗や自律神経などに影響が出て,その体の反応から脳が冷たいものを要求することで,消費行動に繋がることがある,という程度のことです.このように因果関係は基本的にはわからないものの,お互いの変化にある一定の関係が推測される場合に,相関があると言います.以下では実際に求め方を学習します.