- 本日の作業内容
- 漢字書字スピードのデータについて
リンク先のデータは,ある人間がタブレット上で画数が3画から23画までの漢字を手書きした際に要した時間となっています.この人物が一画あたりに要する時間を求めてみることにしましょう.
データをグラフ化したものを図1に示します.
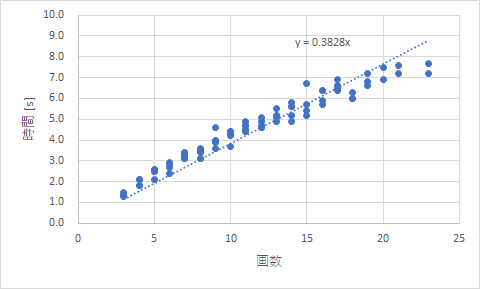
図1 画数と書字時間の関係
どうもあまり良いフィッティングとはなっていないようです.まず,原点を通らない直線でフィットさせるとどうなるか見てみましょう.
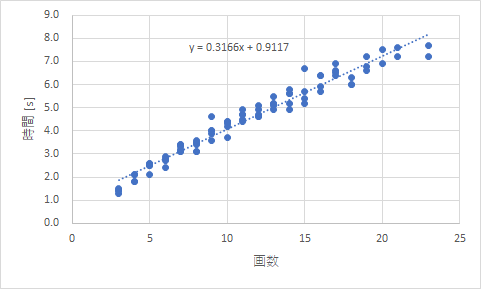
図2 原点を通らない線形近似でフィットした場合
この場合には切片として 0.91 [s] という時間が出てきてしまいます.では,この時間は何なのかということですが,「よーい,スタート」となってから反応して実際に書き始めるまでの時間と考えることも可能です.
ただし,上の図2でも直線とのフィットは今一つですし,反応時間が 0.9 [s] というのも余りに遅すぎる感じですね.つまり,元々のデータが直線ではなく,画数が増えて行くにしたがって傾きが小さくなっている状態のために直線では近似できないと考える方が無難なようです.
では,多項式近似を用いてフィッティングしてみましょう.結果は以下の図3のようになりました.
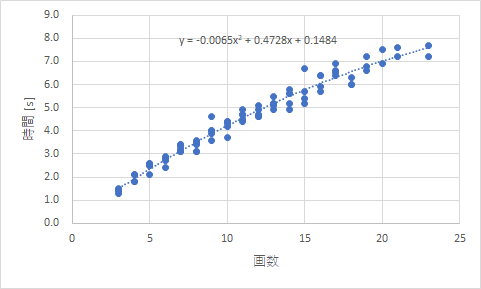
図3 多項式近似
2次の項まで入った結果となりましたが,形としてはかなりよく一致しているようです.では,これで何か解釈ができるでしょうか.
まず,曲線の式を見てみると,以下のような2次式です.
y = -0.0065x 2 + 0.4728x + 0.1484
反応時間が 0.1 [s] 程度というのは常識的な値なので,これは良さそうです.また,1画当たりに要する時間が 0.47 [s] というのも画数の少ない漢字のデータから妥当なように思われます.ということで,結局負の値を持つ2次の係数があることがポイントということになるのでしょうか.
当たり前ですが,一定の面積の枠の中に漢字を書く作業ですので,画数が増えていくと1画当たりの線の長さは短くなります.なので,画数が増えていっても書字する際に指先が動く距離は比例して増えていくわけではありません.そのため,それを制限する負の係数を持った効果が画数が多くなってくるとだんだんと見えてくる,というのが考察としては順当なものではないでしょうかね.基本的には20画くらいの漢字の線の長さは3画や4画の漢字の3-4倍程度にしかなりません.画数で議論することが実は良くないというそもそもの前提が悪い実験だったというオチでした.すみません.
- 放射性元素の半減期
かつて宿題として出したものですが,再び考えてみましょう.まず使用するデータはリンク先のものです.
放射線量が半分になる時間のことを半減期といいますが,今回のデータの場合に半減期がどうなるか,見てみましょう.
- 重力加速度の計算
こちらも一昨年度の授業で宿題として出したものですが,もう一度見てみましょう.データはリンク先のものです.
重力加速度は場所によって異なることが知られています.ある場所で物体の落下実験を行ったとします.実験は 100 [m] の高さから物体を落下させ, 0.2 [s] ごとに物体の高さを計測するもので,結果は添付の表のようになりました.このデータを使用して重力加速度を求めてみましょう.
- 双曲線関数の近似(無理矢理バージョン)
前回の授業で高温での磁化の振る舞いがアロットプロットによって記述されることを説明しましたが,低温における強磁性体(磁石にくっつく物質)の磁化(単位体積当たりの磁気モーメント)は,近似的に以下の式で表されることがあります.外部磁場 H に対して,tanh の形で変化すると記述できる場合があるということです.リンク先のデータがあり,係数 λ を 1 とするとき,自発磁化 M 0 の値を求めてみましょう.
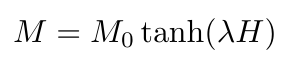
- 次回の予習範囲
今回は残念ながら出来が大変悪うございました.原因は過渡現象の理解ということで,なかなか専門と絡めて議論することは大変なようですね.でも,何のために習ったのか,今一度自省して下さい.
まずは,解答を確認しましょう.
[1] 電流のグラフ
以下のようなグラフが作られるはずです.
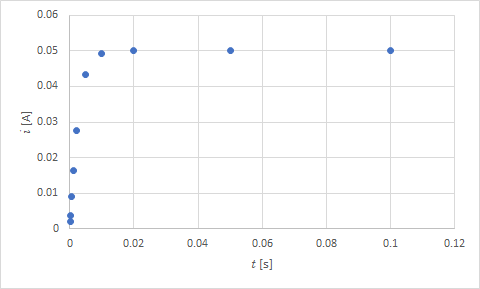
電流の時間変化
[2] フィッティング
「新たにグラフを作る必要が」あるというところが理解してもらえなかったようです.過渡現象は今回のように現実的でない特別に大きなインダクタンスを入れても 10 msec 程度で終わるくらい瞬間的な現象で,インダクタンスは理想的には電気抵抗ゼロなので,時間が経つとただの抵抗だけの回路ですから,一定の電流が流れることになります.そのため,定常電流は 0.05 A ということになりますから,E / R = 0.05 A です.その値から電流 i を引くと,電流の変化分ということになるので,そのグラフを作ります.下のようになります.
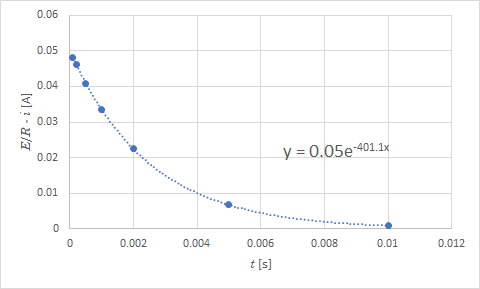
電流の過渡解に対応する変化
ここで,前回の Web テキストで紹介したように値にゼロや非常に小さい値が含まれていると,近似曲線の指数関数が正しく動作しないので,横軸を 0.01 sec までで打ち切りました.
回路理論的にきちんと説明すると,式(1)の両辺に R をかけると,抵抗 R の両端の電位差の時間変化となります.電源の電圧 E からそれを引くと,今度はインダクタンス L の両端の電圧となり,それが上のグラフの変化と同じになります.[3] R と L の値
さきほど E / R = 0.05 A となりましたので,抵抗 R は 200 Ω ということになります.そして,R / L = 401.1 と上の図の式にありますので, L は 0.499 H ということになりました.
では,問題のあるものを見ていきましょう.まずは,グラフに関するものです.
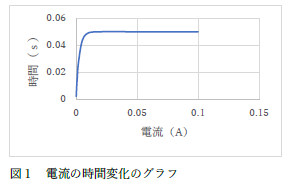
|
何もかもおかしいグラフです.プロット点はない,縦軸と横軸の量も違う. |
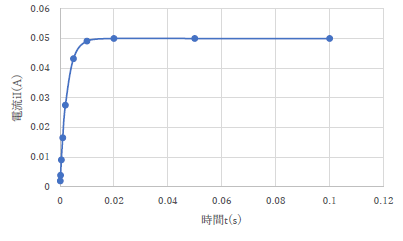
|
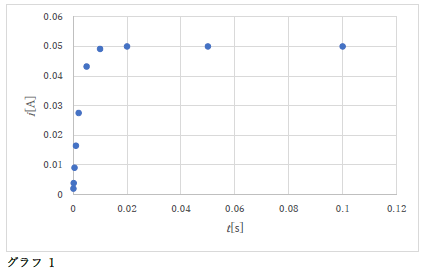
プロット点を繋ぐ線は不要ということは何度か指摘しています.また,このグラフにはキャプションがありませんでした. |
|
図には必ずキャプションをつけましょう.キャプションは通し番号だけでなく,説明も必要です. |
次の2つのようなものが今回ものすごくたくさん出てきました.こういうのは最小2乗法とはいいません.

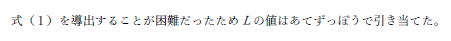
物理量はテキスト中でも数式中でもイタリックでないといけないと何度も説明し,チェックボックスも用意しているのに,がん無視ですか?

最後のは,全く関心できないひどいものです.まず,設問を [1]-[4] まで用意しているのに無視し,説明もなく,図のキャプションもなく,まったく不親切で,人に見てもらおうという気持ちが感じられません.
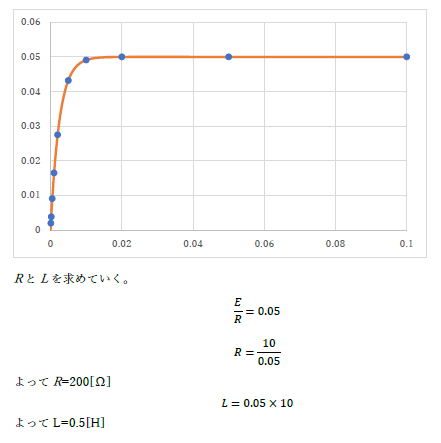
前回も最小2乗法でしたが,指数関数が入るようなより自由度のある形を試しました.今回も引き続き最小2乗法です.結果の解釈も含めて理解が深まるよう演習を行っていきましょう.
資料を参考に予習してください.
次回は t 検定について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは翌週の火曜日の13:00までです.よろしくお願いします.
Back