- 本日の作業内容
- 単純なべき関数
前回の線形回帰で以下のようなべき級数についての場合を実習しました.
y = a + b1 x + b2 x2 + b3 x3 + ・・・
しかし,実際の問題では従属変数 y が独立変数 x の何乗に比例するのか知りたい場合があります.つまり,以下のような式の場合です.
y = a x b
上式のような単純な場合にはグラフに挿入する近似曲線の式で簡単に求められます.例えば,以下のデータは y = 0.7 x 2.5のものです.
x y 1 0.70 2 3.96 3 10.91 4 22.40 5 39.13 6 61.73 回帰の結果をわかりやすくするために関数式通りのデータとしています.
このデータをグラフ化して,前回行ったようにプロット点を右クリックして近似曲線を挿入します.その際には,「累乗」を選択してください.すると,近似曲線が挿入されます.その後で,近似曲線上で右クリックして「近似曲線の方程式を挿入」を選択することで,グラフの中に式が表示されます.その関数形の中の係数が求める変数 a と b です.エクセルでは+ボタンから「近似曲線」→「その他のオプション」で「累乗近似」にチェックを入れてください
なお,この方法では以下のような式については係数を求めることができませんので,注意してください.y = a + b1 x + b2 xm + b3 xn + ・・・
- 異なる形のべき関数
以下のような関数形の場合の回帰はどうなるでしょうか.
y = a b x
両辺の対数を取ると,
log10 y = log10 a + x log10 b
のようになり,直線の式に変形することができます.そこで,表計算ソフトではそのような場合の最小2乗法のために logest() という関数が用意されています.この関数も前回の linest() 関数と同じように結果を表で出す配列表現です.
以下のようなデータセットで考えてみましょう.これは, y = 0.5 * 3.2 xです.
x y 1 1.60 2 5.12 3 16.38 4 52.43 5 167.77 6 536.87 logest() 関数は使い方は linest() と同じですので,先週と同じように作業してみましょう.3つ目の引数は0(FALSE)だと先頭の定数係数を1とし,TRUEだと係数として計算します.きちんと答えが出たでしょうか.
また,この関数形の場合には,グラフから近似曲線を得ることができません.ですので,グラフに近似曲線を引きたい場合には自分でデータを用意する必要があります.
なるべく細かく横軸の値を入れるほうが良いので,例えば,0.2刻みで0.8から6.2まで列のセルを作り,その右に先ほど求めた係数を使用して関数の式を入れ値を作ります.その後で,以下のような操作をすることで近似曲線を追加できます.
- グラフ内で右クリックして「データの選択」を選択
- 「データ系列」タブがアクティブになっている状態で左下の「追加」ボタンをクリック
- 右側の「データ範囲」エリアの「X値」をクリック
- 「X値の範囲」欄の右端のボタンをクリック
- X値の範囲を選択:範囲の部分にX値の範囲を入力
- 同じように「データ範囲」の「Y値」を選択してYの範囲を入力
- 「データラベル」は適当に入力
- 「OK」をクリックすると点プロットの回帰曲線がグラフに挿入される
- 近似曲線のどれかの点を右クリックして「データ系列の書式」を選択
- 「線」タブを選択して「線の属性」の「スタイル」から「実線」を選択
- 右側の「アイコン」で,「シンボルなし」を選択し,「OK」をクリック
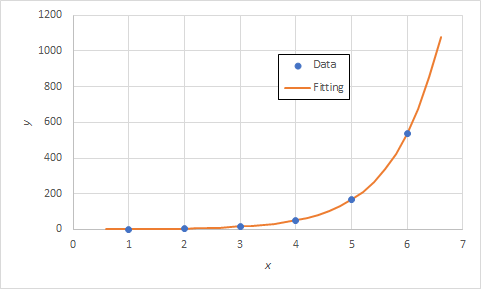
図1 回帰曲線の挿入プロット点の上にフィッティング曲線が重なってしまう場合には,「データの選択」で,赤丸で囲った上向きと下向きの記号を使ってデータ順を変更してください.ただし,ときどき変わらないこともありますorz
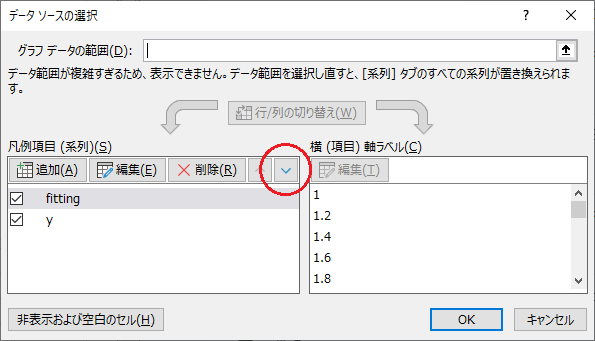
- グラフ内で右クリックして「データの選択」を選択
- 指数関数
指数関数は科学計算では非常に重要なものですが,表計算ソフトでは重視されていません.そのため,グラフから求めることになります.一番単純な形として次の式のときをまず考えます.
y = a e b x
単純なべき関数の時と同様にグラフを作成し,グラフの近似曲線挿入のときに「指数関数」を選択して,その後で近似式を挿入すれば,係数 a と b の値を得ることができます.次の例で試してください.
x y 1 1.34 2 6.03 3 27.01 4 121.03 5 542.41 6 2430.93 指数関数を近似曲線として選択できるのは値に 0 や負の数が含まれないときに限定されますので注意が必要です.また,e-ax の場合は 0 に近い値が含まれるときちんとフィットできない場合がありますので,そのような値を含まない範囲で近似曲線を挿入するなど,こちらも要注意です.
- 多項式の指数関数
次の式を考えます.
y = a +b x + c e d x
最小二乗法は基本的には線型結合の多項式しか扱えませんので, x の項と ex の項があるとそのままでは適用できません.試しに以下のデータについて,指数関数で近似関数を求めてグラフにするとあまりフィットしません.
x y 1 30.56 2 36.47 3 44.72 4 58.17 5 83.22 6 134.06 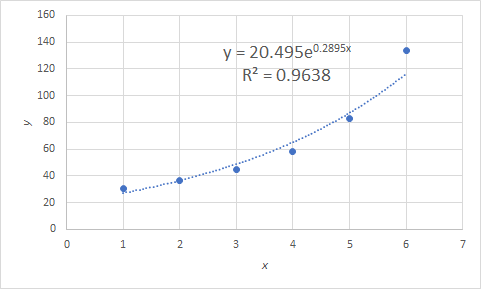
図2 多項式の近似曲線推定そこで,一度変数変換して z = e xとし,以下のように表を作り直します.
x z y 1 2.72 30.56 2 7.39 36.47 3 20.09 44.72 4 54.60 58.17 5 148.41 83.22 6 403.423 134.06 式としては
y = a + b x + c z
という形ですので,先週行った linest() で最小二乗法が適用できます.
e の肩の x の係数が消えてしまいますが,今回はそこは目をつぶりましょう.
上のように表を作りなおして,最小自乗近似を行って近似曲線を作りなおすと次のようなグラフを作成できました.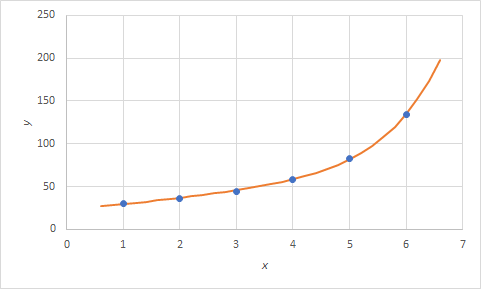
図3 改善した近似曲線これでももしズレが大きいようなら z = e k x のように目分量で変数kを入れて表を作るという強引な方法もあります.
- 演習
磁石にくっつく物質である「強磁性体」の磁気の強さを表す「磁化」についての作業を行ってみましょう.内容は難しい物性の話ですが,とりあえず作業は簡単なので,やってみてください.
強磁性材料は温度を上げていくと,その磁気的性質が徐々に失われていき,ある温度以上では強磁性でなくなります.すなわち磁石にくっつかなくなります.代表的な強磁性体である鉄ではおよそ1000K,コバルトで1400K程度で強磁性でなくなります.
強磁性体の磁化の大きさは外部から磁場を加えて材料がどれくらい磁化したかで測定しますが,高温で磁化が小さくなるとなかなか磁化が飽和しなくなり,きちんとした測定ができなくなります.典型的な磁化曲線と高温で磁化が小さくなったものを図に示します.なお,磁化の単位ですが,任意単位 arbitrary unit a.u.ですので,あまり意味はありません.
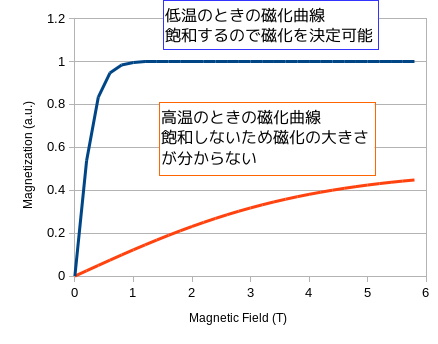
図4 磁化曲線の概念図高温の時には磁化 M は以下のような関数で近似されます.ここで,H は磁場で A,B および C は定数です.
A M 3 - B M = C H
かつては計算機などありませんでしたので,この式から値を求めることは困難でした.そのため,グラフ用紙に M 2を H / M に対してプロットすることで H = 0 に外挿して M の値を求めることを行っていました.それをアロットプロットと呼びます.
さて,以下のようなデータが得られた時,磁化の大きさ(任意単位)を求めてみましょう.
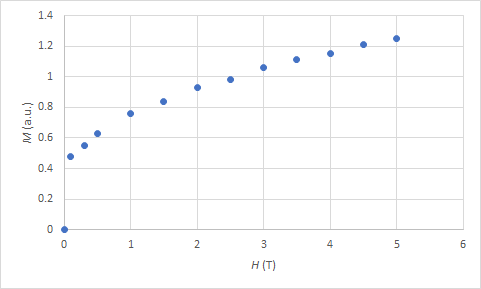
図5 キュリー温度近くにおける磁化曲線H (T) M (a.u.) 0 0 0.1 0.48 0.3 0.55 0.5 0.63 1.0 0.76 1.5 0.84 2.0 0.93 2.5 0.98 3.0 1.06 3.5 1.11 4.0 1.15 4.5 1.21 5.0 1.25 アロットプロットを完成させると以下の図6のようになりました.
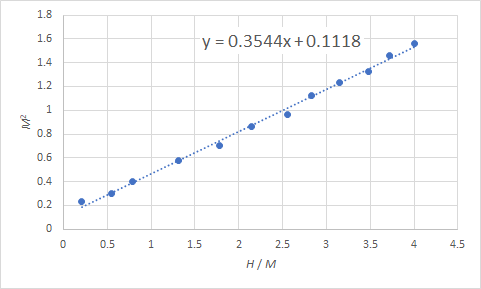
図6 アロットプロット完成図と近似直線図6中の式にあるように,この場合の磁化は 0.33 ということになります.
- 次回の予習範囲
毎年のことなのですが,最小2乗法が始まると成績が一気に落ちます.そうならないよう Web テキストに記述を加えたり,授業中に説明したり,また,チェックボックスなども用意しているのですが,だいたい悪い方に期待は裏切られます.残念です.
では,まずは解答です.先週の授業でも説明しましたが,課題の3次式は2次の項が無いので,エクセルの近似曲線機能は使えません.そのため,LINEST関数を使用して求めます.作業は簡単で,結果としては以下の式が求まります.
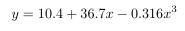
上式を使用して描いた曲線をグラフに加えると下のグラフが得られます.
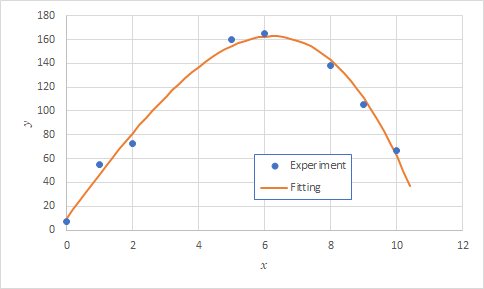
では,皆さんの提出の中で何が問題だったのか,順に見ていきましょう.
|
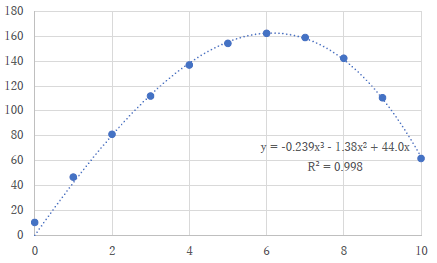
今回最も多く出て来た間違いが左のようにエクセルの近似曲線を使用したものです.また,このグラフを作った人の大半はLINEST関数を使用して正しい数式は求めていました.それなので,その式でグラフを作れば良かったんですが,なぜそうしなかったのか,疑問です.表示された数式には2次の項がしっかりとありますので,題意に反していることはすぐにわかるはずなのですが. |
|
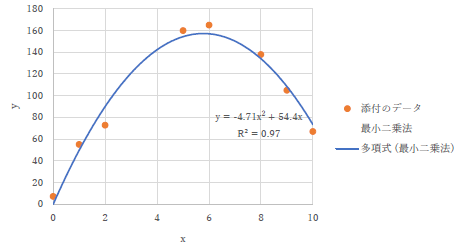
中には,左のように2次関数でフィッティングを行っているものすらありました.もうどうしてなのか,私にはわかりません. |
|
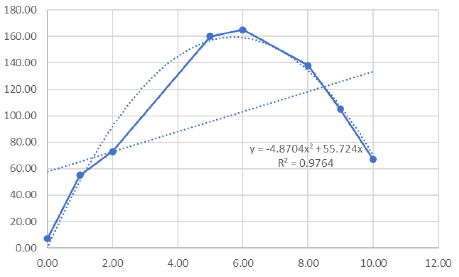
あれやこれや,余分なものばかりがあります.また,実験プロットを折れ線で繋ぐ意味もありません. |
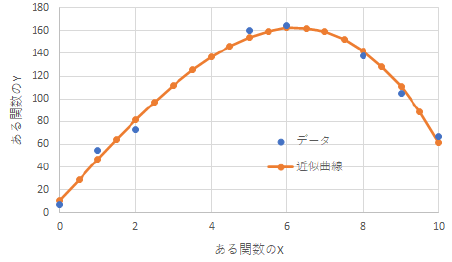
|
左のグラフは,フィッティング曲線にシンボルが入っていることが問題です.近似曲線は連続関数ですので,特定のプロット点はありません. |
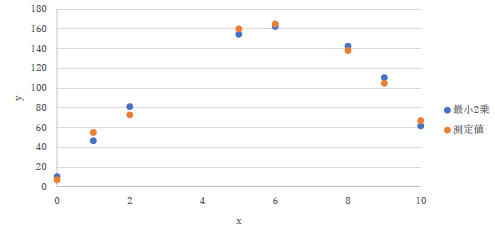
|
左のものも上と似たような間違いです.近似曲線は連続した線で入れてください.データを細かく取ると,折れ線グラフでもきちんとしたものに見えます. |
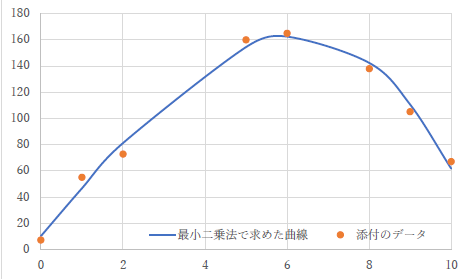
|
左のものも,近似曲線がおかしいものです.もっと細かく点を取って行かないと,本来の3次関数の形になりません. |
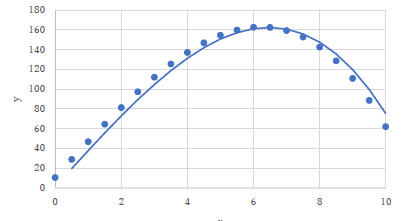
|
これは意味がわかりません.なんなんでしょうか? |
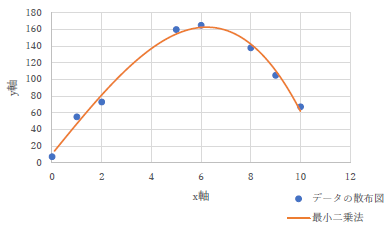
|
通常,縦軸と横軸の説明に「x 軸」とか「y 軸」とか,書きませんよね? |
以下は数式や文章についての間違ったものです.こちらはチェックリストを用意したのですが,結構無視する人が多かったのが残念です.
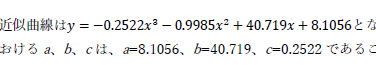
|
有効数字について一応警告は出していたのですが,ダメでしたね.何桁取るのか,基本的には結構難しいものがありますが,今回は y の値を参考に3桁程度は見込めるという想定でした.2桁で回答した人も特に減点などはしていません. | |
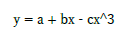
|
べき乗の表現はちゃんと上付きの機能を使用してください. | |
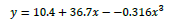
|
負号は連続して使えませんよね? | |
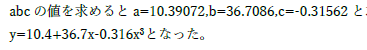
|
イタリックになっていません. | |
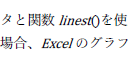
|
EXCELのような「名称」はイタリックにしません.また,プログラミング言語やデータ処理ソフトなどでは関数はイタリックになりません.フォントもだいたいCourier などを使用することになっています. | |

|
3次関数という指定があったのに,「放物線」でいいんですか? | |
前回は線形回帰を求める最小二乗法について学習しました.表計算ソフトでは linest() という関数が用意されていて,それを使うと簡単に回帰直線や回帰曲線が求まります.ただし,前回のマティーセンの法則のように途中の次数の項がが飛ぶような場合には,グラフの方から回帰曲線ではきちんとした近似にはならないこともあるので,注意してください.
今回はより一般的な関数系についての最小二乗法です.
資料を参考に予習してください.
資料の方にあるように科学技術関連の実験データの解析にはべき乗や指数・対数など物理的な背景を反映した理論式と比較する場合が多くあります.しかしながら表計算ソフトはビジネス向けに基本的には開発されているので,そのような目的に適した関数はあまり準備されていません.ですので,少し工夫が必要です.
以下では基本的な関数系であるべき関数と指数関数,対数関数について回帰曲線を求める方法を試してみましょう.
次回も最小2乗法について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは翌週の火曜日の13:00までです.よろしくお願いします.
Back