- 本日の作業内容
- 原理式からの算出
予習用の資料の(1)式のように,結果が y = a + bx の直線式に従うことが予想される場合には,誤差の2乗和を最小にすることで,式(15)により係数が求められることがわかります.この(15)に従って作業してみましょう.
先ほどの図1は以下のデータをプロットしたものです.
Voltage (V) Current (mA) 0.1 11 0.3 20 1.1 58 1.2 73 1.8 89 2.5 112 3.1 197 3.7 303 係数を出すために必要な和はΣx2,Σx,Σy,Σxyですので,それらを求めれば算出できます.以下のような値となるはずです.
a = -15.87 b = 71.74 y = -15.87 + 71.74x
- 回帰直線の式を使う
表計算ソフトには回帰曲線を求めるための関数も用意されています.今行っている線形回帰では直線の式ですので,傾きと切片を求める関数slope()とintercept()で計算できます.数式を実際に入力して求めてみましょう.関数ウイザードを使用すると,データ範囲などを案内してくれますので,わかると思います.
- 決定係数
統計的な分析では「決定係数」(Coefficent of determination)という値が使われることが多くあります.この値(R2)は独立変数(説明変数,通常は横軸の変数)が従属変数(非説明変数,縦軸の変数)のどれくらいを説明できるかを表すとされており,通常は以下の式で計算されます.
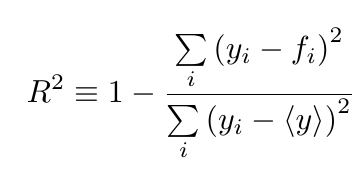
ここで, f は推定値,<y>はyの平均値です.
上の例ではR2の値は0.90となり,割りと高い値です.
- より高度な近似式の求め方
slope()とintercept()を用いる方法は,y=a+bxという式の傾きと切片を求める方法でした.しかしながら,原理的には切片が0になる線形の関係式で計算したい場合があります.そこで,一般的な線形回帰式を求めるための関数linest()というものが用意されています.
LINEST(既知のY(yの範囲),既知のX(xの範囲),定数,補正)という引数仕様です.「定数」の部分はTRUE(0以外の値)だと切片あり,FALSE(0の場合)には切片なし(原点を通る)です.
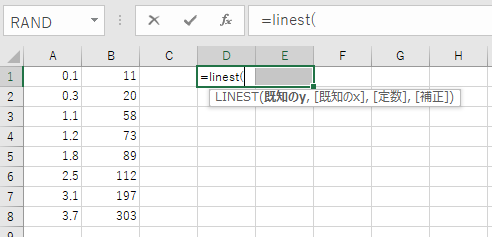
図2 LINEST 関数の入力仕様まず線形の部分を0,補正の部分も普通に0にして,Enterを押して確定してみましょう.65.57という値が表示されたのでは無いでしょうか?これが原点を通る直線の場合での傾きとなります.
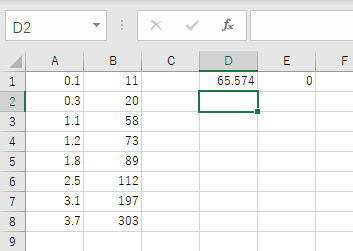
図3 切片を0としたときの,LINEST 関数の実行結果切片を 0 でない数にし,補正も入れると以下のような結果となります.
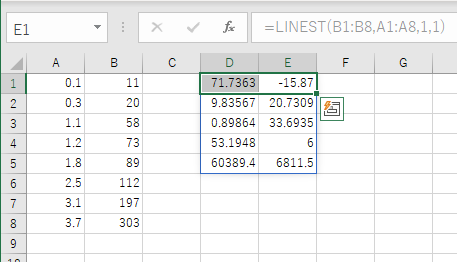
図4 原点を通らない設定での実行結果大量の数値が結果として出てきましたが,ここでは基本的には1番上の行だけ使うことになります.それぞれのデータの意味は,Microsoft の Excel サポートページによると以下の通りです.
傾き 切片 傾き(係数)の標準誤差 切片(定数)の標準誤差 決定係数 r 2 y の値の標準誤差 F 補正項 自由度 df 回帰の平方和 残差平方和 よくわからない言葉が並んでいると思います.これらの用語については,実は注意が必要です.というのも,最小2乗法による実験値による曲線のフィッティングと回帰曲線は,似たような作業で求めるものの,意味が全く違うということです.
今回行っているのは,最小2乗法で,その大原則としては,実験値を説明する理論式はあるものの,係数などは未定であるのでフィッティングにより係数を決定する作業であるということです.一方,回帰曲線は,実験値から曲線(1次関数の場合は直線)の形自体を決定するということです.上の表で出て来た自由度や平方和は回帰分析で使用するもので,今回の最小2乗法では使いません.
- グラフへの近似曲線の挿入
グラフに近似式の直線を挿入してみましょう.グラフエリアをダブルクリックしてグラフ編集をアクティブにし,データプロットをクリックして右クリックで出てくるメニューから「近似曲線を挿入」を選びます.デフォルトでは回帰の種類が左上の「線形」になっているはずなので,そのまま先ほど計算した直線が描画されます.原点を通るものに変更する場合には,「オプション」の中の「切片を設定」にチェックを入れ,値を0とすれば原点を通る直線に描き換えられます.
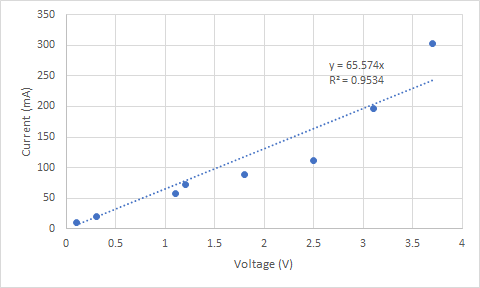
図3 回帰直線の描画EXCELは科学技術データ用のアプリでは無いために,グラフに入れられる近似曲線の機能はずいぶんと貧弱です.そのため,単純な直線や単純なべき関数や指数関数などでしか使用できません.万能ではなく,使えないものがあることを理解しておいてください.
- 各種作業
以下に示す作業を行ってみましょう.
- 中性子の個数
リンク先にあるのは原子番号と原子量(既知の元素のみ)の対応表です.正電荷を持つ陽子どうしを結合させるために必要な中性子は,陽子1個あたり何個になると推定されるか,求めてみましょう.
実験値と計算値の両方をグラフにまとめてみましょう.
かつてこれをレポート課題にしたときに,実に多くの人の解答が間違っていたので,注意しましょう.最終的に求めるのは,上にあるように,正電荷を持つ陽子どうしを結合させるために必要な中性子は,陽子1個あたり何個になると推定されるか,です.
- 多項式近似
リンク先のデータはある金属の電気抵抗率の温度依存性です.マティーセンの法則によれば金属の電気抵抗はデバイ温度以下の極低温で以下の式となります.式の係数を求めてみましょう.
ρ = ρ0 + αT + βT 2 + γT 5
高次の項を入れるには,linest()関数のXの範囲の部分にべきの項を追加します.n次までだとすると以下のようになります.
数式の入力が終わったら,Enterで確定させて下さい.そうすると,配列数式という形式になり,5次の項の係数,2次の項の係数,1次の項の係数,定数項となり,近似式を求めることができます.#N/A(N/AはNot Applicable)は今のところは無視して大丈夫です.
LINEST(既知のY(yの範囲),既知のX(xの範囲)^{1,2,3,…,n}, 定数,補正)
べきの次数は連続でなくても飛ばしでも可能です.今回は1次,2次,5次ですね.こちらについても,グラフに結果をまとめてみましょう.
- 中性子の個数
- 次回の予習範囲
課題のアップロードが今回は遅れてしまってすみませんでした.直前にもかかわらずたくさんの提出がありました.皆さんの頑張りや意気込みに感服しました.以後気をつけます.
で,学生実験のレポートを提出した人がいました.ちゃんと実験の方の提出ができたのか,心配です.提出時間は証拠として残っているので,何かあったら私の方からも担当者に説明しますので,言ってください.
以下は問題のあるものの例です.参考にしてください.まずはグラフに関するものです.
|
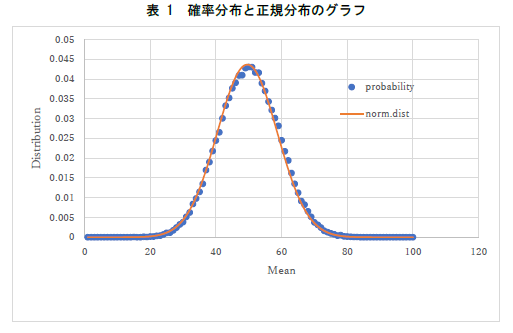
図のキャプション(説明)は図の下に置きます.また,このグラフは x 軸の最大値が120ですが,これは今回は有りえない値なので,適切ではないですね.データのプロット順も問題で,正規分布の曲線が,データプロットの上(手前)に来ています.実験点が見づらくなるので,通常はデータ点などのシンボルは曲線や直線の上(手前)に来るようにします. |
|
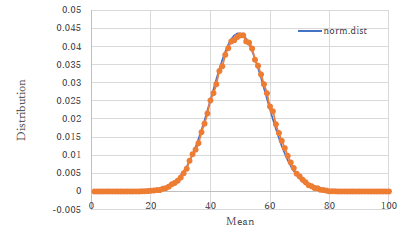
縦軸の最小値が有りえない負の値になっています.これも以前に指摘したように不適切な軸の取り方です. |
|
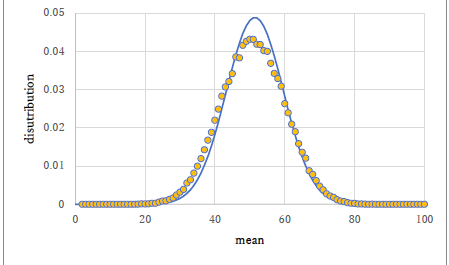
こんなにデータプロットと正規分布曲線がずれることはありません.どちらか間違っています. |
次は文章に関するものです.
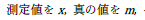
|
|
|||

|
|
|||

|
|
|||
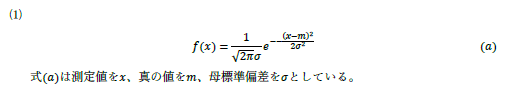
|
作業課題 [1] 全体でこれだけの記述というのはやはり不十分です. | |||
最後に紹介するのは,また今回も出て来た残念なものです.やっつけ仕事というやつですかね.んで,グラフの方はプロット点と連続曲線の使い方が逆になっていますしね.
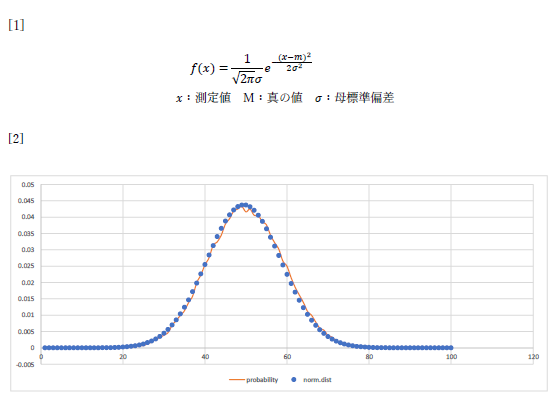
ところで,今回の数式ですが,上の例のように e の肩に負号を持つ分数がある場合,単純に数式エディタで負号 - に続けて分数を置くと,パッと見にくっついて見えてしまうようです.授業資料の方は数式を美しく表示するために元々開発された組版ソフトの LaTeX を使用しているので,それなりにきれいに見えるのですが,マイクロソフトの数式エディタではその辺りの質が落ちるようです.そこで,意図的に負号 - の次にスペースを入れるとより分かりやすくなります.今後の参考にしてください.
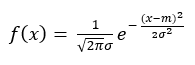
正規分布について学習しました.関数としてはnorm.dist()をメインで使用しました.引数を4個も取るのですが,それぞれ中身を理解して今回も使用しましょう.特に,最後の引数はFALSEならば確率密度関数の値を,TRUEであれば積算を返すことはよく覚えておきましょう.
資料を参考に予習してください.
実験において,基本的な原理が明らかとなっており変数の関係が数式的に表現できるようなデータの組を得ることができる場合には,実験結果のグラフに関係式に基づいた近似曲線を描くことができます.例えば,図1に示すような実験結果が得られた場合などです.
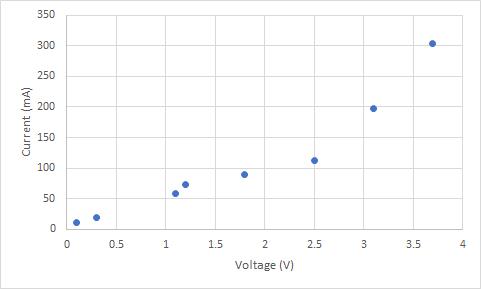
図1 グラフの例
実験結果を整理する場合,図1のようなグラフのプロット点を折れ線でつなぐことには全く意味がありません.背景となる理論が不明の場合(実際にはよくあることですが)にはスムーズな線で結ぶことを行います.一方で前述のように原理が明らかで関係式が既知の場合には,その関係式をプロットして理論と実験の結果の比較が可能です.
しかしながら,通常の実験では操作したパラメータによって理論式の係数やべき級数の展開次数などが変わる場合があり,そのような場合には実験結果と最もよく合うようにそれらの係数を選ぶことが実験の目的だったりします.
最小二乗法とは,結果に最もよく合う係数などを決めるための手法です.実験値には必ず誤差が含まれていますので,理論式との誤差が最も小さくなる係数を探します.誤差は正と負の両方があるので,誤差の2乗和を最小にすることが必要ですので,最小二乗法と呼ばれます.また,それにより求めた曲線の式を回帰式と呼ぶ場合があります.今回は最小二乗法の中で最も基本的な線形回帰について学習します.
次回も最小二乗法について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは授業翌火曜日の13:00までです.よろしくお願いします.
Back