- 本日の作業内容
- 正規分布を扱う関数
まず,自分で正規分布関数のグラフを作成しましょう.平均値0で,標準偏差が1の標準正規分布を描きます.使用する関数は norm.dist() です.Normal distributionから関数名が来ています.
関数ウイザードを使用すると,指示が出てきますので,それに従ってグラフを作成してください.
また,正規分布は確率密度関数ですので,その全範囲にわたって積分すると1になります.それを求めることも norm.dist() 関数を使用してできます.図1のように,正規分布の形と累積度数のグラフを作ります.
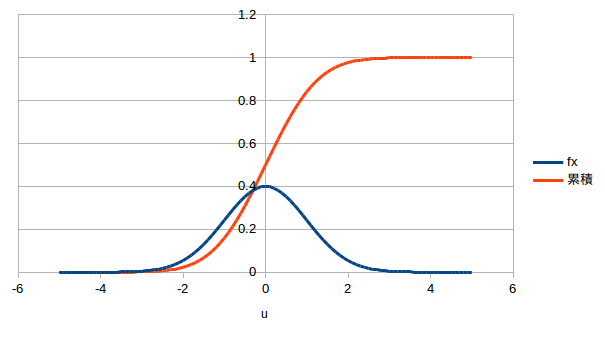
図1 標準正規分布の形と累積度数横軸の変数 u は,-5から5までの範囲を0.1刻みで作って見ました.
実は,標準正規分布関数については,平均値などを入力しなくても良い norm.s.dist() というものが用意されています.上の例であれば,そちらを使っても構いません. - 前回のデータの分布
前回の作業で,0から99までの乱数を10回発生させて平均値を取る作業を10回行って,平均値の平均値を取る作業をしました.その時に得られた10個の平均値と平均値の標準偏差を用いて,乱数の平均値の分布図を作成しましょう.
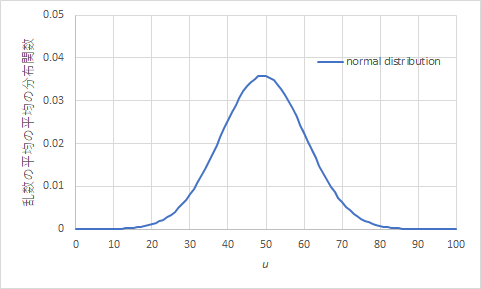
図2 前回の乱数の平均の平均の分布norm.dist() 関数には平均値と標準偏差を引数として与えます.
- 積算度数の意味
元々の乱数は0から99のどの整数も等しい確率で出てくる「離散一様分布」というものでしたが,平均値の分布は正規分布とみなしても良いものになります.(中心極限定理)図2を見ると,平均値の平均値が,例えば30くらいになることはかなり低い確率となりそうです.では,どの程度の確率でそうなるのか,やはり norm.dist() 関数を用いて確認してみましょう.
関数の引数の4番目を1にすると,積算を計算してくれます.試しに図2の結果で試してみると,0.042という値となりました.これは,30以下の平均値になる確率が4.2%であることを意味しています.また,70以上になることもほとんどなさそうですが,実際に確率を計算で求めてみましょう.
- パーセンタイル値
積算度数は,注目する値が小さいほうから見てどの程度の場所にあるのかを示す量ですが,それをパーセント表記したものをパーセンタイル値と呼び,記号 %ile で表します.その値が小さいほうから見て全体の何%のところにあるのかを示すものですが,実際に人が操作するシステムでは,操作盤の高さやスイッチの配置などで,想定するユーザの身長など5%ileから95%ileの範囲内の人における操作のしやすさなどを考慮することがあります.
- 実際のデータによる分布の推定
文部科学省が毎年調査している体格データの最新版(学校保険統計調査R3年度)では,17歳の状況は以下の表のようになっています.
表1 身長・体重データ
男 女 身長 (cm) 体重 (kg) 身長 (cm) 体重 (kg) 平均値 標準偏差 平均値 標準偏差 平均値 標準偏差 平均値 標準偏差 170.8 5.90 62.4 10.45 158.0 5.39 52.5 7.70 これらのデータが正規分布になるとしたときに,どのような分布曲線となるか,図2のような曲線によるグラフを作りましょう.
また,当時の自分の身体データのパーセンタイル値を積算度数から調べてみましょう.
- 中心極限定理の確認
これまで見てきたように rand() 関数によって発生させた乱数は離散一様分布になります.これが,その平均値が実際に中心極限定理により正規分布になるのかを確認しましょう.
大量のデータが必要になりますので,今回もC言語もしくはPythonのプログラムを利用して,作業を行います.次に示すプログラムは0から9までの整数を乱数により10回発生させ,その平均値を求める作業を100回行うものです.まず,データをこれにより作成しましょう.データの保存方法は以前に行ったように,実行結果をリダイレクトして行います.
C言語版#include <stdio.h> #include <stdlib.h> #include <time.h> int main(void) { srand((unsigned) time(NULL)); int i, j, sum; for(i=1; i<=100; i++) { sum = 0; for(j=1; j<=10; j++) { sum += rand() % 10; } printf("%d, %f\n", i, (double) sum / 10); } return 0; }> .\a.exe > data.csv ← PowerShell もしくはコマンドプロンプト
$ ./a.out > data.csv ← VS Code (WSL)
Python版import random for i in range(1,101): add = 0 for j in range(1,11): add += random.randint(0,9) print('%d, %.1f' % (i, add / 10))> python data.py > data.csv
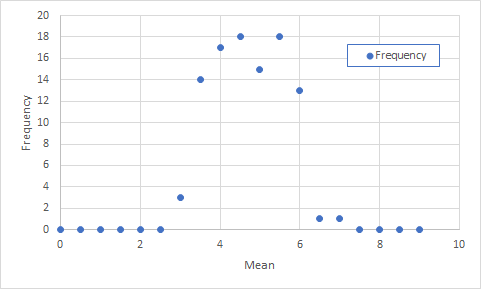
図3 中心極限定理の確認その1上のグラフ作成のためのデータ処理は以下のように行っています.
- 横軸用のデータ
度数分布を取るので,横軸はある範囲で区切って用意することになります.ここでは,0.5刻みです.すなわち,0,0.5,…,8.5,9というように18個のセルを作成しました.
- 度数を求める
以前 countif() 関数を用いて度数を求める作業を行いました.そのときは,隣のセルと数値が一致するかどうかだったので引数も単純でしたが,今回は不等号を使用するのでちょっと複雑です.
=COUNTIF(B$1:B$100,"<="&D4)-COUNTIF(B$1:B$100,"<="&D3) まず,元々の平均値のデータがB1からB100のセルに入っているとします.それらのセルのうちで,左隣のセルに入っている値(例えば1.5)以下の平均値の個数をひとつ目の countif() で数え,次にその値から一つ上のセルの値以下の平均値の個数を2つ目の countif() で数えて引いています.Excelのようなセルを用いた方式ではわかりづらいかもしれませんが,この上の式は漸化式になっています.
countif()の中で不等号で比較するときには,不等号を二重引用符 " " で囲い,さらにデータセルの前に記号の & をつける必要があります.
- グラフ
グラフは散布図で作成しています.
エクセルには標準で度数分布を作成できる「ヒストグラム」の機能がありますが,使用が面倒なので,今回は手作業で行うことを想定しています.興味有る人は自分で調べてみてください.
- 横軸用のデータ
- より大量のデータによる確認
一様分布から正規分布に形が変わっている様子は先ほどの作業で確認できました.ただ,まだ凸凹しています.そこで,より多くのデータを用いて作業を行ってみましょう.
以下のプログラムは0から99までの乱数を10回発生させて平均値を取ることを10万回行って,平均値の分布をグラフ化するためのデータ作成を行うプログラムです.実行すると,グラフにすぐ読み込める形式で度数を計算していますので,確認してみましょう.
C言語版#include <stdio.h> #include <stdlib.h> #include <time.h> #include <math.h> int main(void) { srand((unsigned) time(NULL)); int i, j, sum, count[100]; double ave[100000], sum_x = 0, sum_x2 = 0, mean, stdev; for(i=0; i<=99; i++) { count[i] = 0; } for(i=0; i<=99999; i++) { sum = 0; for(j=1; j<=10; j++) { sum += rand() % 100; } ave[i] = (double) sum / 10; } for(i=0; i<=99; i++) { for(j=0; j<=99999; j++) { if(ave[j]>i && ave[j]<=i+1) { count[i]++; } } } printf("mean,frequency\n"); for(i=0; i<=99; i++) { printf("%d, %d\n", i+1, count[i]); } for(i=0; i<=99999; i++) { sum_x += ave[i]; sum_x2 += ave[i]*ave[i]; } mean = sum_x / 100000; stdev = sqrt((sum_x2 - mean * mean * 100000) / 99999); printf("\n\n\nmean,%f\n", mean); printf("stdev,%f\n", stdev); return 0; }
Python版import random import math count = [0 for i in range(0,101)] av = [0 for i in range(0,100000)] sum_x = 0 sum_x2 = 0 for i in range(0,100000): add = 0 for j in range(1,11): add += random.randint(0,99) av[i] = add / 10 for i in range(0,100): for j in range(0,100000): if av[j]>i and av[j] <= i + 1: count[i] += 1 print('mean, frequency') for i in range(0,100): print('%d,%d' % (i + 1, count[i])) for i in range(0,100000): sum_x += av[i] sum_x2 += av[i] ** 2 mean = sum_x / 100000 stdev = math.sqrt((sum_x2 - mean ** 2 * 100000) / 99999) print('\nmean, %f' % mean) print('stdev, %f' % stdev)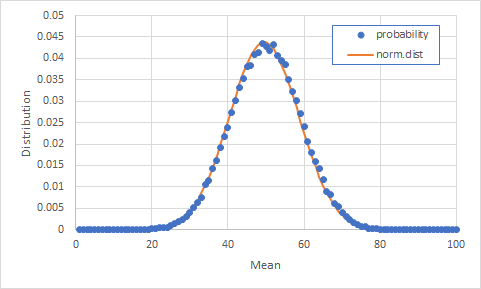
図4 確率分布と正規分布の比較図4ではプログラムの実行結果の度数の部分を確率に直し,プログラムの最後に計算してある平均値と標準偏差を用いて正規分布のグラフも作成して比較してあります.
- 次回の予習範囲
今回初めてちゃんとした形式のレポートということになりましたが,残念ながらいろいろと問題が多く見られました.この後解説して行きますが,まずは本来の結果です.
私のところで実行すると以下のようなグラフが得られました.
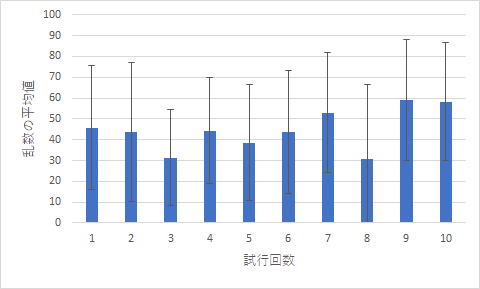
|
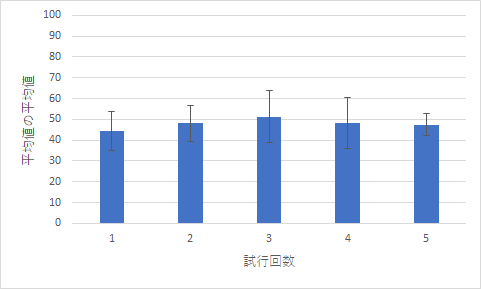
|
|
| 図1 10回の乱数の平均値 | 図2 10個の平均値を5回集めた平均値 |
では,いくつか見ていきましょう.まずはグラフに関係するものです.
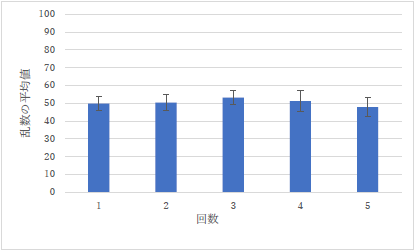
|
何人かで見られました.エラーバー(誤差範囲)がこんなに小さくなることはたぶん無いので,やり方を間違えています.また,縦軸の「乱数の平均値」も適切ではありません. |
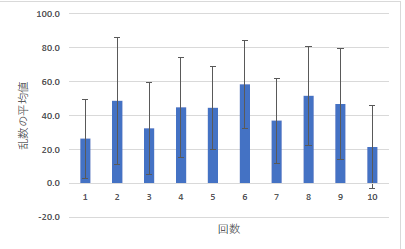
|
前回も説明しましたが,今回は負の値が出ることは無いので,縦軸は 0 から始めないといけません.エラーバーが長くなったので,EXCELが勝手に-20にしていますが,はやりグラフは 0 から始めましょう. |
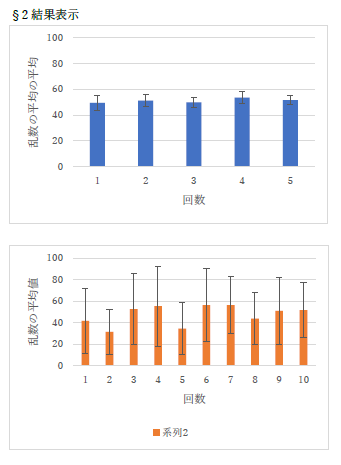
|
グラフの順番も間違えているし,説明もないし,エラーバーは間違っているし. |
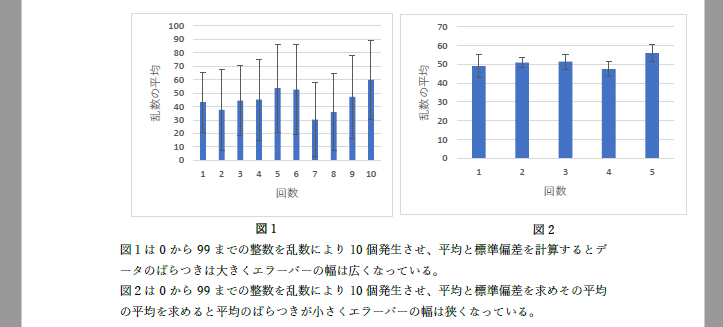
上のものは,図が本来の余白をはみ出しています.電子データとして見るから問題ないように見えますが,はやり余白はちゃんと確保してください.
今度は数式に関するものです.
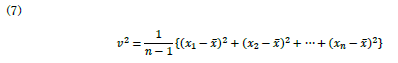
|
違うことをやっていますね. |
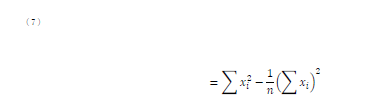
|
これもちょくちょく見られたのですが,式に左辺が無いですよ? |
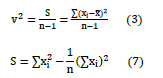
|
数式エディタを使用すると,通常は量を表す記号は斜体(イタリック)になるはずなんですが,なんで立体(ローマン)なんでしょうか? |
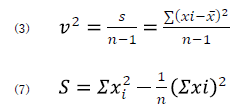
|
下付きになっていない添字 i があります. |
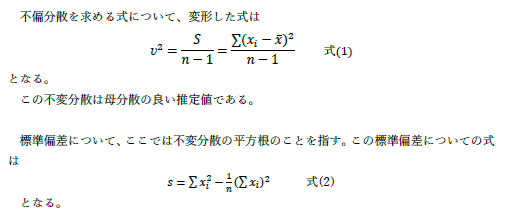
|
一つ目の式は数式エディタで独立したボックスで作成してあるのですが,2つ目は,行内に挿入する形式になっていますので,記号や表現がコンパクトになってしまって,見た目が違ってしまっています. |
本文でもいろいろと問題が見られました.
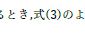
|
なかなかわかりづらいと思いますが,読点の「,」が半角文字「,」になっています.日本語の表記としては,全角の「,」を使うか,「, 」のように半角の読点の次に半角スペースを入れるか,どちらかを使います. |
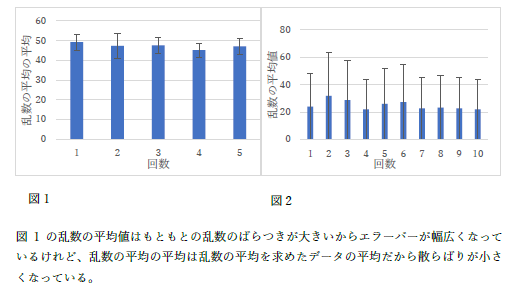
|
説明している文章と図が違います. |
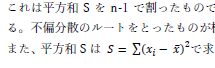
|
「平方和 S 」の「S」がイタリックになっていません.他にも文中の n もイタリックになっていません.文中でも量を表す記号はイタリックで無いといけません. |

|
こっちは今度は数字がイタリックになってしまっています.「n-1」の部分ですね.数字はイタリックにしませんので,注意してください. |
最後に,その他の問題点です.
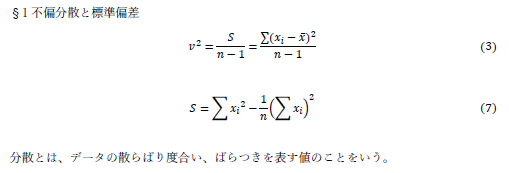
|
説明になっていません.分散は記号は何で式はどれでしょう?文中に記号を使用してきちんと説明していないものは,減点としています. |
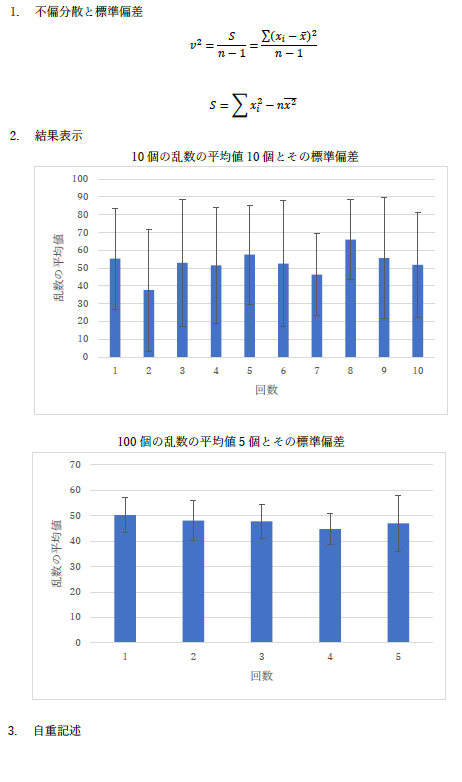
|
はいはい,言われた作業はやりましたよ.ってな,ふざけた失礼な内容ですね.さすがに 0 点とはしませんが,ほぼ 0 点です. |
確率分布に関する作業と,グラフ作成や数式作成についての作業を前回は行いました.グラフでは標準偏差を求めることで,エラーバーのついたグラフの作成ができるようになりました.また,平均値の平均値を取ることで,標準偏差が小さくなる(理論上は1/√N)となることも確認しました.表計算ソフトの機能は使わないと忘れてしまうので,学生実験のレポートや各授業の復習の際に使用して自然と作業できるようになってください.
リンク先の資料を参考にしてください.
また,標準正規分布表も参照できるようになっています.
次回は「最小2乗法」について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは翌週火曜日の13:00です.よろしくお願いします.
Back