- 本日の作業内容
- ばらつき確認
- 乱数発生
今回も乱数を発生させて,バラつき具合を見ていきましょう.まず,0から99までの整数を乱数により10個発生させ,その平均値と標準偏差(不偏分散の平方根)を計算します.そして,その作業を10回繰り返して,各回の平均値と標準偏差を求めましょう.
- 基本グラフの作成
次にそのグラフを作成します.棒グラフで10個分の平均値を表示させましょう.そして,今回新たに学習するのは,標準偏差をグラフに入れることです.
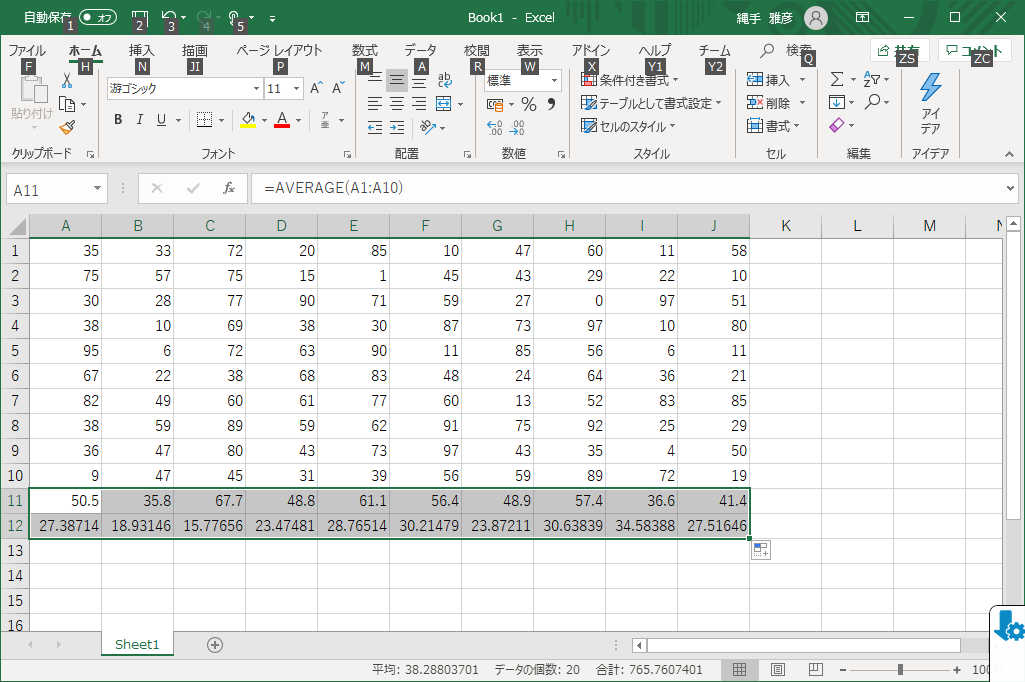
まず,今回は「4.グラフ要素」も使って,縦軸と横軸の量も表示させます.例えば,縦軸は乱数の平均値,横軸は回数とすると,図1のように作成できます.
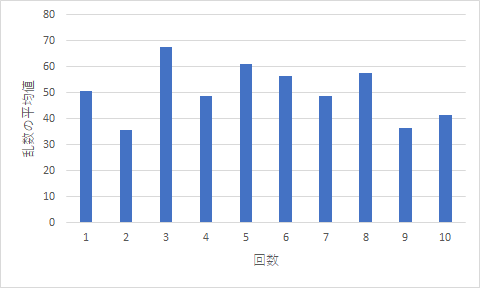
図1 乱数の平均値のグラフ - エラーバーの挿入
では,標準偏差をこのグラフに入れる作業に移りましょう.まず,グラフの中をクリックして,編集モードに入ります.左上の「グラフ要素の追加」メニューを選ぶか,グラフ右上の+ボタンをクリックするかして「誤差範囲」を選択し,右向きの▲マークをクリックして次の階層に進みます.「その他のオプション」を選んでください.棒グラフのマークのタブを選んで設定していきます.
縦軸誤差範囲: 両方向(B)
誤差範囲: ユーザ設定(C)「値の指定(V)」をクリックし,「正の誤差の値(P)」の右にある上矢印↑をクリックして,表の標準偏差が入っている10個のセルを選択し,Enterキーを押します.同じように「負の誤差の値(N)」も同じエリアを選択します.
OKボタンをクリックすると標準偏差分の長さの棒が正側と負側につきました.図2のようになっていることでしょう.
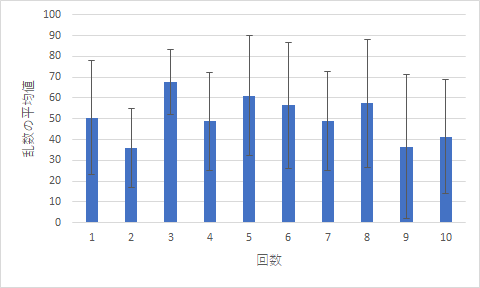
図2 エラーバーがついたグラフもし最小値が0でなかったら,そちらも0に修正してください.
さて,この授業では複数回エラーバー付きのグラフの作成を行いますが,その際に毎年必ず間違ったエラーバーのつけ方をする人がいます.その原因はだいたい決まっていて,以下の図のように作業をしているようです.
どこで間違えたかというと,グラフ右上のボックスから「グラフ編集」「誤差範囲」と進んで,その後安直に「標準偏差」を選んでいることです.
このとき標準偏差を選択すると,表示しているグラフの棒の値の標準偏差を挿入します.それは一つの値しか無いので,棒グラフに付いた全てのエラーバーの値が同じになり,異様な感じです.
他にも「標準誤差」を選択して,均一な短いエラーバーが付いているような間違いもちょくちょく見られます.
必ず「その他のオプション」を選んで,自分で表から値を選択してエラーバーをつけてください. - 別のデータ作成
同じような作業をしてもらいますが,10個の乱数を発生させ平均値を取る作業を10回行って,10個の平均値の平均値を求める作業をしてください.さらにその作業を5回繰り返しましょう.そして,同じくそれら5回分の平均値とエラーバーを表示させるグラフを作成します.随分エラーバーが短くなったと思います.
予習用資料にあるように,n個の平均値の標準偏差は元々の標準偏差の√n分の1になりますので,それを確認してください.最初に行った10個の乱数の標準偏差と,10個の平均値5個の標準偏差を比較しましょう.
- 乱数発生
- 数式エディタ
不偏分散を求める式(3)とその変形の式(7)を作成しましょう.以下のような手順で作成します.
- 数式エディタの起動
Wordを起動し,「挿入」メニューからΩの「記号と特殊文字」を選択し,πとある「数式」を選択します.メニューが出てきますので,「新しい数式」を選択して数式入力を始めましょう.
- (3)の作成
メニューアイコンが上の方にたくさん出てきますので,それらを利用して数式を入力していきます.
v2 の場合には ex とある「上付き/下付き文字」を,分数は x/y の「分数」を,Σは「大型演算子」を,そして,平均値を表すxバーはä「アクセント」を利用します.
手書きでの数式認識機能もありますので,必要に応じて使ってみてください.あまり評判はよくありませんが.
- (7)の作成
同様に数式を作成しましょう.
- 数式エディタの起動
- 課題
課題については,授業の最後に案内します.
レポート形式の文書を作成してもらいます.以下のような構成とします.
計測工学基礎 レポート 2023.4.26 学生番号:S226099 氏名:松江花子 §1 不偏分散と標準偏差
このセクションでは式(3)と式(7)を貼り付けて,分散について簡単な説明を行う.§2 結果表示
今回行ったバラつき作業に関する2つのグラフを貼り付け,結果に関する簡単な説明を行う.§3 自由記述
この授業への感想(や苦情),現時点でのExcelについての自分の理解度を自己評価により記述し,今後自分がどのようにこの授業に取り組んでいくつもりか,その心意気を記述する.レポートはPDF形式のファイルを提出してください.「ファイル」メニューから「エクスポート」の機能を使用してPDFに変換できます.
今回は4つのグラフをPowerPointなどに貼り付けて一つのファイルを作成するということで,作業しているうちに自分の学生番号と名前を入れるのを忘れた人が多数いました.残念ですが,減点しました.レポート提出システムによる提出なので個人の特定はできましたが,以前の紙での提出であれば,採点されませんね.注意しましょう.
さて,結果としては以下のようなものになるはずです.
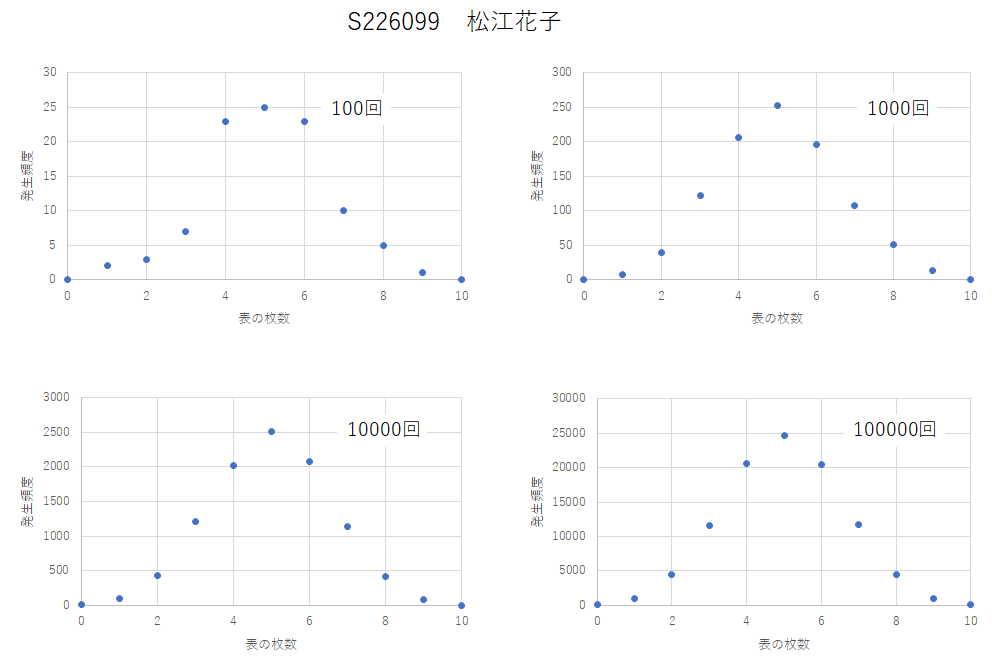
今回縦軸の説明の表現で気になるものがこれまた多数ありました.例えば,「表の出た回数」とか「表の出た頻度」などです.これは正しく量を表しているものではないので,ちょっと減点しました.こういうことにも注意を向けるようにしましょう.
以下は,問題のあるものの一部です.コメントを付けていますので,今後の参考にしてください.
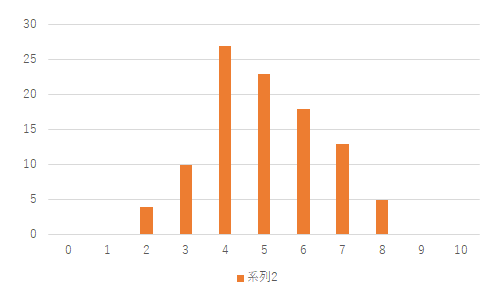
上のものはエクセルのデータを選択してグラフを書きました,はい終わり,というものですね.何を表すものなのか,見てもらう人にわかるよう敬意を払うということが一切無いですね.合格点はつけられません.
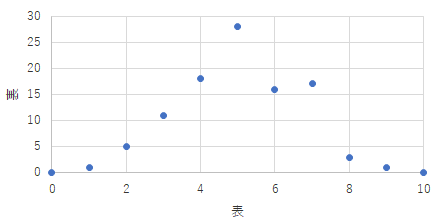
上のものは,縦軸と横軸の量の説明が間違っています.これでは意味が通じません.
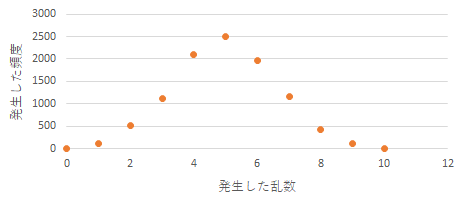
一見正しいようには見えます.これはエクセルでグラフを作成して軸の範囲をそのままにしているところで,ちょっと問題があります.今回の横軸になるのは10枚のコインを投げた時の表の枚数です.それは0から10までしか存在しません.横軸が12まであるのは不適切です.
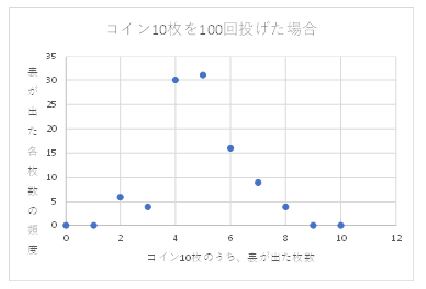
推測ですが,小さな図を後から拡大してのではないでしょうか.ドットが荒く汚い図になっています.で,それは置いておいて,縦軸の量の説明ですが,横書きとするのが科学技術系のグラフの常識です.
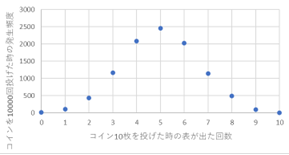
縦軸の説明が長くなってしまいました.それでも上下のバランスを考えて,中央に揃えるようにしてください.
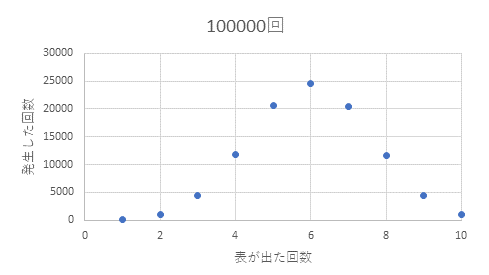
上のものはどうしてプロットが横にずれたんでしょうかね?6枚が最も多いというのはすでに変だと気づきませんでしたか?プロットが1から始まっているので,グラフ作成において間違いがあります.
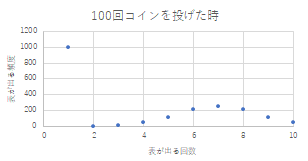
こちらは4枚のグラフのうちのこれだけが間違っていました.100回コインを投げたのに,表が1枚というのが1000回もあるというのはおかしいと思いませんでしたか?また,他のところも200回超えたりしているので,データの選択がおかしいですね.
データのバラつきについて学習しました.表計算ソフトで使用可能な統計関数はたくさんありますが,その内の分散と標準偏差について実際に扱いました.基本的には以下の区別がわかっていることが重要です.
| var() | 不偏分散 |
| var.p() | 標本分散 |
| stdev() | 不偏分散の平方根(標準偏差) |
| stdev.p() | 標本標準偏差 |
リンク先の資料を参考にしてください.
次回は「正規分布」について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.今回まではWeb上で事前に内容をお知らせしていますが,次回以降は以下のように内容の公開と提出期間を設けますので,よろしくお願いします.
公開:原則水曜日18:00
締切:原則翌週火曜日13:00
Back