- 本日の作業内容
- グラフの横軸や縦軸に量の名称を入れる
前回の内容で乱数の出現頻度の棒グラフを作りましたが,縦軸や横軸には何も説明が無い状態まででした.それでは人に説明するためのデータにはなりませんので,まずそれらを入れることから始めましょう.
前回グラフを作成した表をもう一度使用します.
- グラフ要素の追加
前回の授業で作ったグラフをダブルクリックします.そうすると,上のメニューバーがグラフモードに変わり,左上に「グラフ要素の追加」メニューが出てきます.それを選択すると「軸ラベル」という項目が出てきますので,それを選びます.
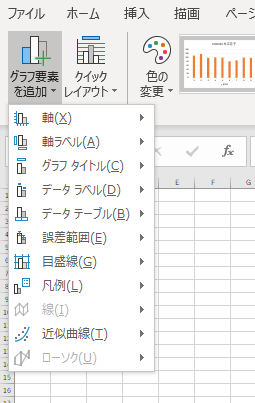
さらに縦軸と横軸を選択するようになりますので,それぞれ作業をしましょう.
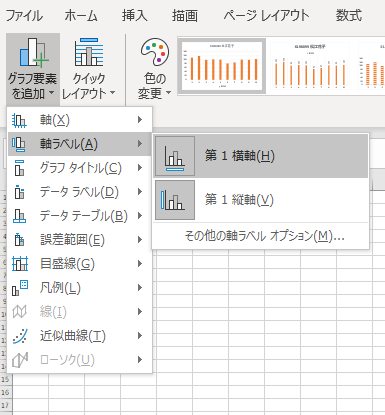
- 仕上がり
「軸ラベル」という四角い入力エリアが出てきますので,その軸ラベルという文字を消して適当な項目名を入れると,下図のように出来上がります.
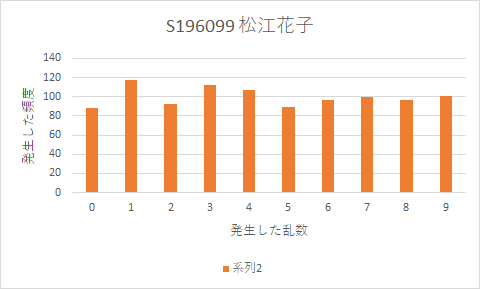
- ショートカット
軸ラベルの追加の操作は,グラフの右上に表示される+の四角をクリックすることで現れるメニューからも可能です.お好きな方をお使いください.
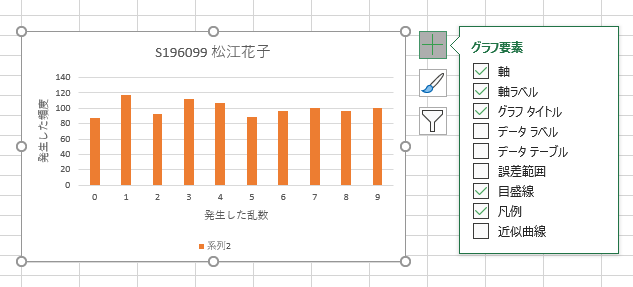
- グラフ要素の追加
- 平均値を求める関数average()
ここからはいくつか関数を使用する練習です.実験データの整理などで必須の平均値から使ってみましょう.
値や個数は何でもいいので,適当にいくつかのセル(縦か横に1列に並んでいるものが良い)に数値を入れます.次に,それらのセルの最後のセルの次の位置に平均値を求める関数average()を入力して,先ほどの数の平均値を求めましょう.average()は単純な算術平均を求めるものです.
- 分散を求める関数var()
先ほどの数値のバラつき具合を見ます.バラつきの度合いは分散という量で示すことができます.関数ウイザードを見ると,分散にはいくつかの関数が用意されています.
関数名 内容 VAR 不偏分散 VAR.P 分散 VAR.S 不偏分散 VARA 不偏分散 VARAP 分散 VARAPA 分散 データの中身が数値でなかった場合など細かいところもありますが,基本的には「不偏分散」か「分散」かの違いです.var()とvar.p()がどう違うのか,実際に値を求めてみて,授業資料にある定義(式(1)などを使うと実際に求められます)と絡めて考えてみましょう.
- 残差平方和を計算する関数
自習資料の式(1)の残差平方和を求める関数がEXCELには標準で備わっています.まずは,それを体験してみましょう.以下のデータで試します.
残差平方和を求める関数は devsq() です.それを用いて上の演習用データの残差平方和 S を求めてみましょう.
- 標本分散
式(1)の標本分散を求めましょう.
- 不偏分散
式(3)の不偏分散を求めてみましょう.
- var() と var.p()
分散を求める関数var() と var.p()を使って,演習用データの分散を求めてみましょう.
- 残差平方和を計算する関数
- 標準偏差を求める関数stdev()
分散は次元が実際のデータの2乗となってしまうので,直接値を見ても感覚的にわかりづらいものがあります.そこで,分散の平方根を取って標準偏差とすることで値を考えやすくなります.ここでも,関数ウィザードで見るといくつかのタイプがありますが,分散と同じように考えることができます.stdev()とstdev.p()で何が違うのか,実際に値を求めてみて考えてみましょう.
先程求めた標本分散と不偏分散と標準偏差関数の対応を確認してください.
- 前回の度数分布のばらつき
先週行った作業で,乱数により0から9までの整数を100回,1000回,そして10000回発生させました.でた回数は当然トータルの回数が少ないほどばらついていました.そのバラつきについて,標準偏差を求めて比較して考えてみましょう.
- 二項分布によるバラつきの確認
データのばらつきは経験則として,真の値に近いほど標本の数が多いということが知られています.真の値から大きく外れるようなばらつきは個数としては少ないということです.また,真の値よりも大きな標本と小さな標本の個数もだいたい等しくなることが知られています.
そこで,二項分布によって,その傾向を確認しましょう.2項分布とは2つの状態のどちらかがランダムに出てくる場合に従う分布で (a + b)n の係数で表されます.
例えば,コイン10枚を投げた場合,表と裏が何枚かずつ出ます.5枚表になる場合が一番頻度が高くて,枚数が偏るほど頻度が少なくなりますが,無限回数投げると綺麗な左右対称系に分布してくるようになります.それを体験してみましょう.
今回はコイン10枚を100回投げる場合,1000回投げる場合,10000回,さらに10万回投げる場合の4通りをシミュレートしてみましょう.さすがにCalcの機能で行うのは大変なので,プログラムを使って自動化しましょう.
- プログラムの準備
- C言語の場合
昨年度までの学科のプログラミング授業はC言語を使用していましたので,まずはC言語版です.
- プログラム
以下のソースを使うと,10回コインを投げて表が出た回数について0枚から10枚まで何回あったかを出してくれます.これを使って元データを作りましょう.
#include <stdio.h> #include <stdlib.h> #include <time.h> int main(void) { int coin[11][5]; int times[4] = {100, 1000, 10000, 100000}; int i, j, k, count; for(i=0; i<=10; i++) { coin[i][0] = i; for(j=1; j<=4; j++) { coin[i][j] = 0; } } for(i=0; i<=3; i++) { for(j=1; j<=times[i]; j++) { count = 0; for(k=1; k<=10; k++) { count += rand() % 2; } coin[count][i+1]++; } } printf("Number of Head, 100, 1000, 10000, 100000,\n"); for(i=0; i<=10; i++) { for(j=0; j<=4; j++) { printf("%d,", coin[i][j]); } printf("\n"); } return 0; }S22の学生さんはまだ習っていない配列が出ているので,とりあえずは使うだけで構いません.
コマンドプロンプトなどで実行すれば結果が得られますが,そもそもどうやってプログラムを動かすかというところはネットなどを参考にして挑戦してください.すみません.
ところで, if 文が無いことにも注意してくださいね. - データ作成
プログラムをコンパイルして実行すると,結果が画面に表示されるだけです.これをデータとして保存するために,コマンドラインでリダイレクトという機能を使います.作業は簡単です.
> .\a.exe > data.csv
とすると,data.csvという名前のCSV(comma separated value)ファイルができていますので,EXCELでそれを開くと値を読みだすことができます.
昨年度のプログラミング入門IIで使用したWSLの場合は以下のコマンドになります.
$ ./a.out > data.csv
- プログラム
- Pythonの場合
今年度から学科のプログラミング言語はPythonに変わりました.現在同時進行しているプログラミング入門IIでもPythonを使用しています.ということで,Pythonのプログラムだと以下のようになります.
- プログラム
import random coin = [[j if i ==0 else 0 for i in range(0,5)] for j in range(0,11)] times = [100, 1000, 10000, 100000] for i in range(1,5): for j in range(1,times[i-1]+1): count = 0 for k in range(1,11): count += random.randint(0,1) coin[count][i] += 1 print('Number of Head, 100, 1000, 10000, 100000') for i in range(0,11): for j in range(0,5): print('{}, '.format(coin[i][j]), end = '') print() - データ作成
Pythonの授業でもちょっとだけ触れましたが,ターミナルでリダイレクトを使用して実行すればCSVファイルをすることができます.VS Code やコマンドプロンプトで以下のようにコマンドで実行してください.
> python coin.py > coin.csv
- プログラム
- C言語の場合
- グラフ作成
バラつき具合をグラフで確認しましょう.グラフの形式は任意ですが,本日実習した縦軸や横軸の説明をきちんと入れてください.
- 課題
前項のコインの表裏のグラフを作成して前回と同様にPNG形式の画像で提出してください.提出にはレポート提出システムを利用してください.
昨年度にもこの課題を課したのですが,かなり多くの人が4つの結果を1つのグラフにまとめていました.そうすると,だんだん正規分布に近づいていくことが視覚的に理解できませんので,注意してください.
PowerPointなどを活用して,グラフをまとめて画像を作りましょう. - プログラムの準備
前回の授業は久しぶりに対面で実施しました.その結果,前年と同じ課題なのに,評価が大幅に上がりました.その場で適宜アドバイスできたことが要因かとも思いますが,昨年度までのオンデマンドでは締切り直前に,きちんと作業せずいい加減なまま出したものが多かったと推測されます.オンデマンドの弊害が出てしまったかもしれません.
さて,今回は問題のあるものはわずか3件でした.以下のようなものが出ていましたので,今後はこのようなことが無いように注意しましょう.
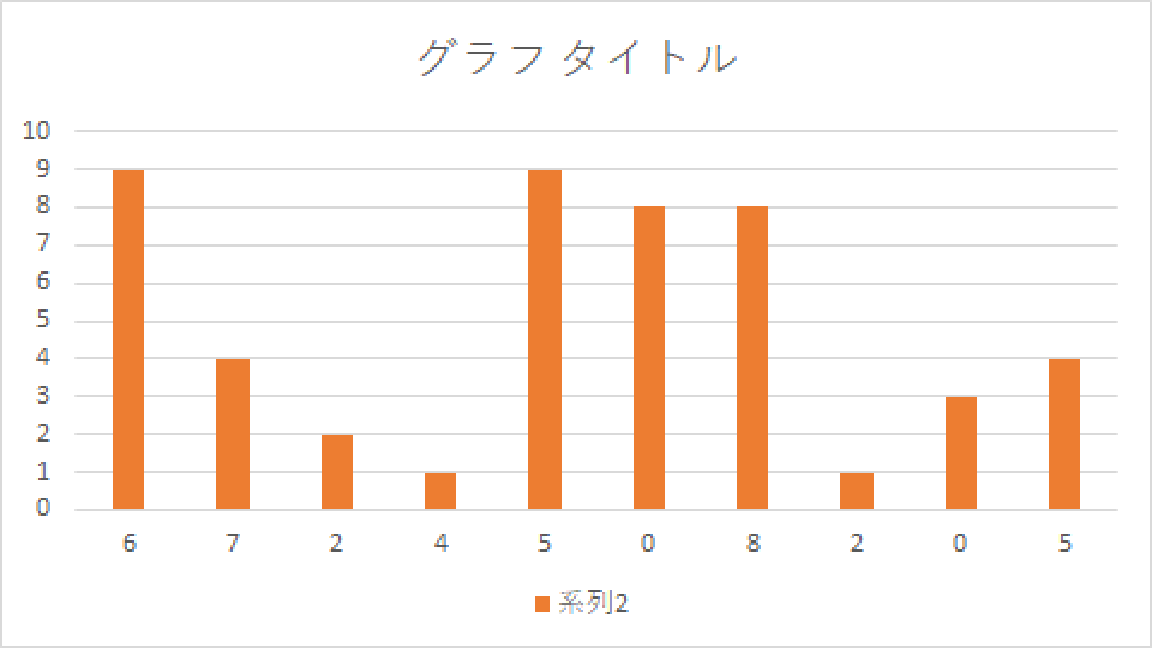
|
まったく何も理解していないまま作ったグラフですね.どうしてこういうのになったのか,よくわかりません. |
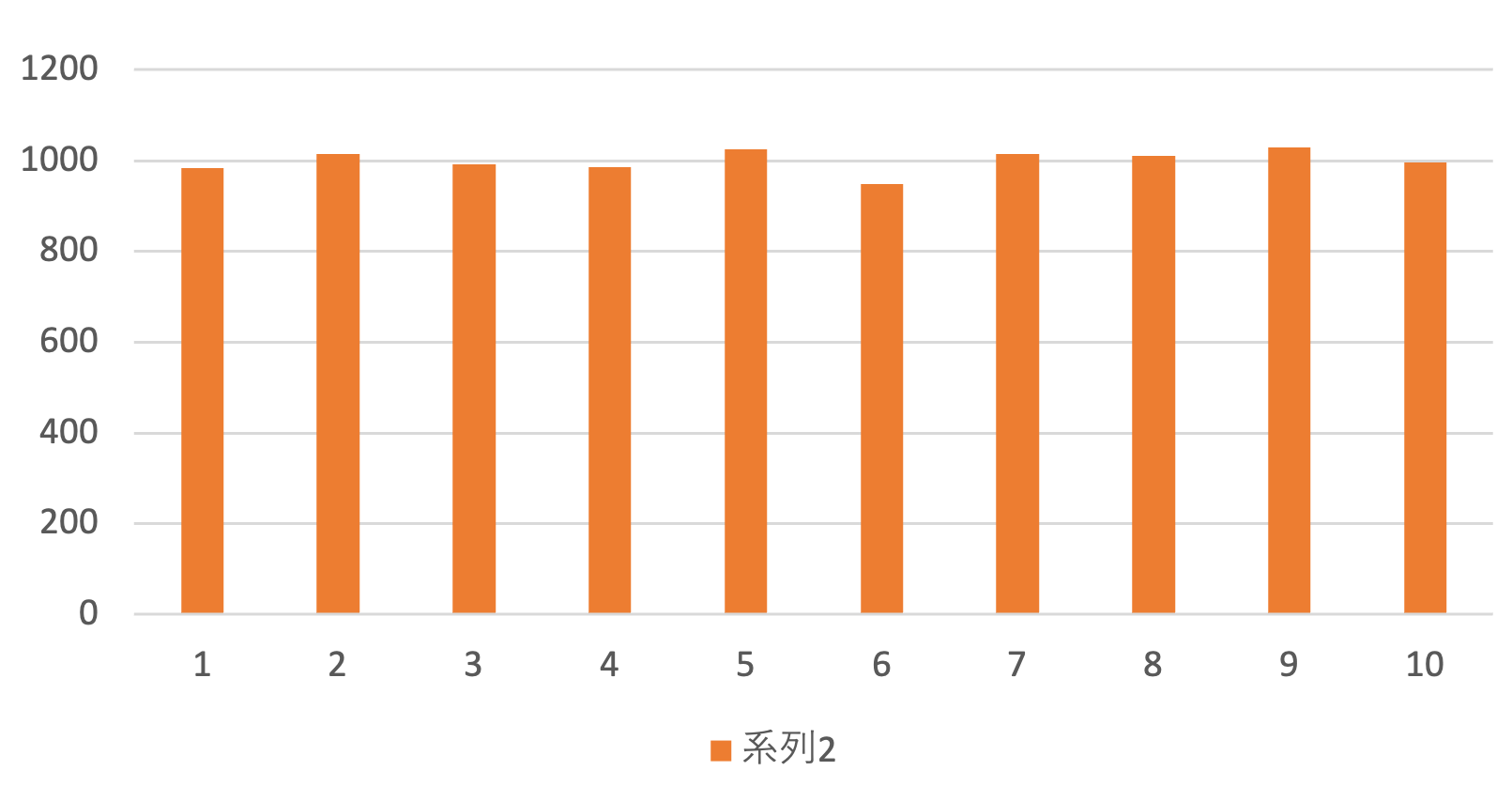
|
横軸はちゃんと発生した乱数にするよう,方法まで書いていたんですけどね. |
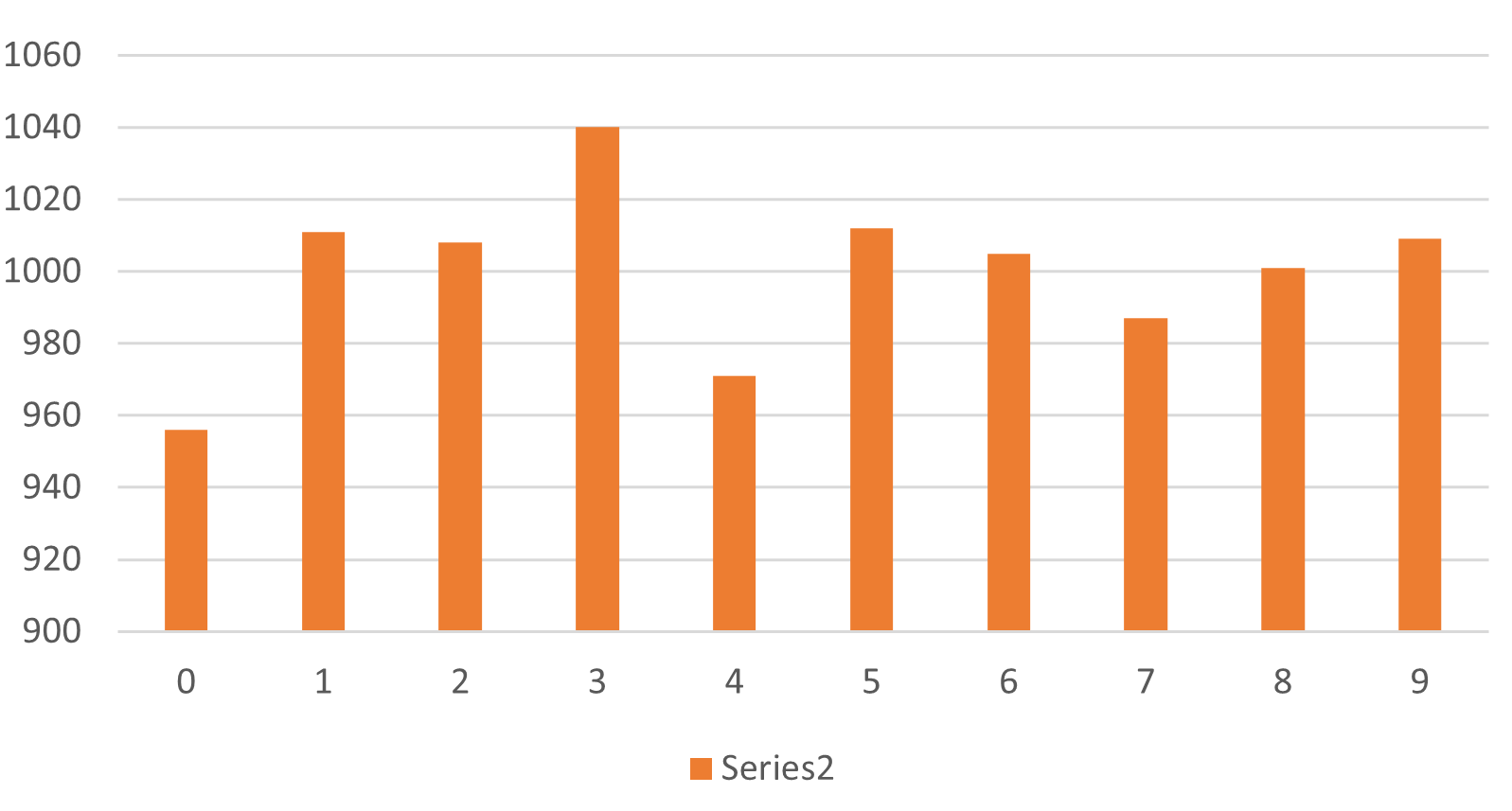
|
縦軸についても,ちゃんと原点から表示するよう,指示していたんですが... |
で,毎年のように画像が鮮明でない人が結構いますし,今回もまたかなりいました.どういう状況かというと,下のようなものです.
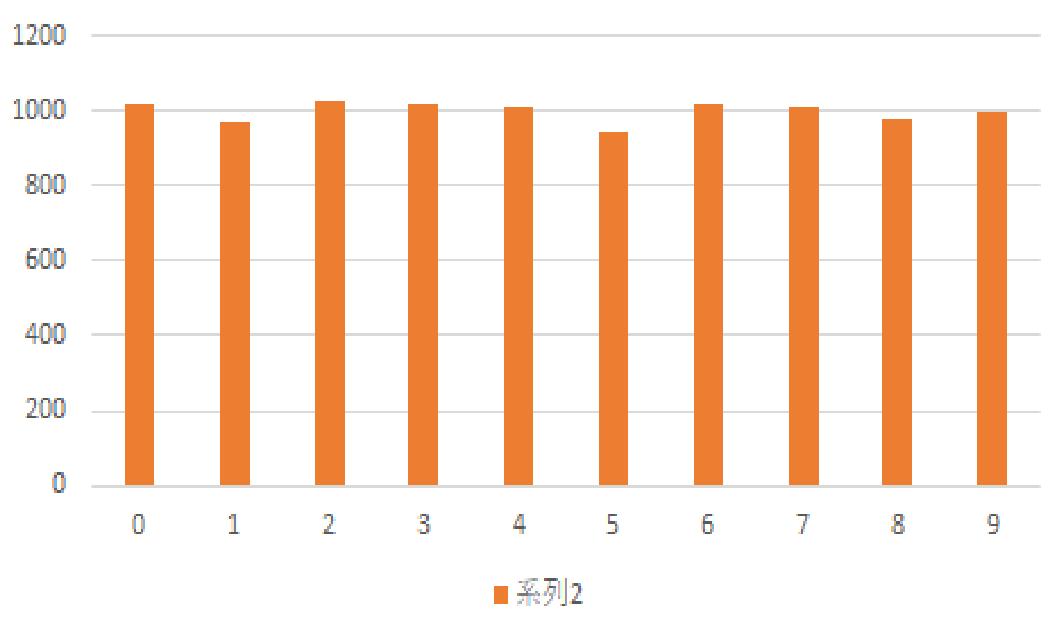
普通に作ると,下のようになるはずなのですが.
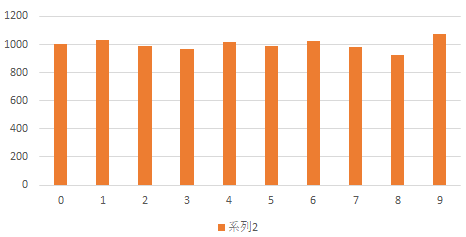
現状考えられる理由は,EXCELからグラフを貼り付けたあと,不要な拡大処理を行ったとしか考えられません.ペイントの方に貼り付けただけだと,ちゃんと下のグラフのようにきれいにできるはずなんですが,何で拡大したんでしょうか?
リンク先の資料を参考にしてください.
次回も引き続き.「分散」や「標準偏差」などの統計量について学習します.今回の資料を参考に予習してください.
Back