- 本日の作業内容
- t分布
これまで統計的に考える際に標本値は正規分布に従ってばらつくということを説明していました.正規分布であるかどうかは大量の標本の値が知られていて母集団がすでにわかっていることを前提にしています.すなわち,母平均と母標準偏差がわかれば正規分布の形を決めることができます.
しかし,資料の方にも書いたように,実際の製造現場ではなるべく少ないサンプルで品質のチェックをしたいのが本音です.そこで,標本が少ない数でも統計的に扱えるようにゴセットが考えたのがt分布です.何が違うのかというと,母平均がわかっておらず,母標準偏差も未知であるという前提で,標本平均と不偏分散の平方根である標準偏差をパラメータにして確率密度関数を作りなおしたものです.
ということで,まずはt分布の形を確認してみましょう.使用する関数は t.dist() です.引数仕様は,値と「自由度」と「関数形式」です.正規分布の時には平均値と標準偏差が必要でしたが,今回はそれは未知なので使用しません.その代わりに自由度を使用します.自由度が1〜8までのt分布を標準正規分布と一緒にグラフ化したものを図1に示します.まずは,これを作成してみましょう.
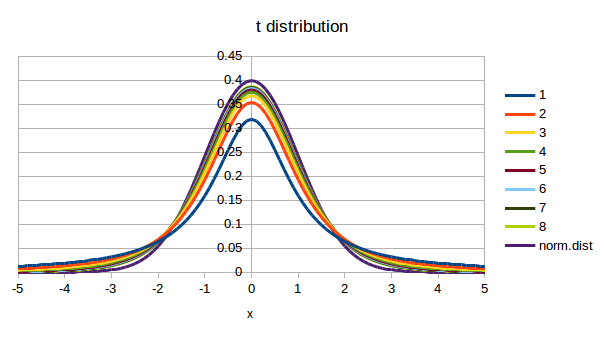
t分布の形正規分布に比べて中央付近が低く,周辺部の値が大きめになっています.なお,自由度を無限大にすると,正規分布と一致します.
- t検定の練習
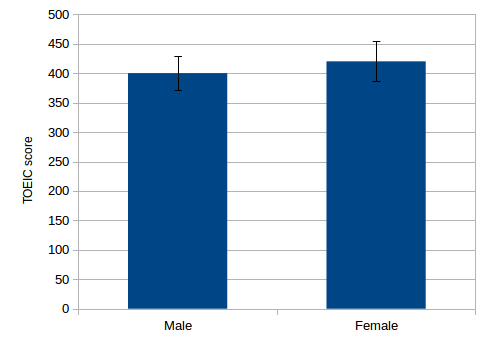
先ほどのTOEICの点数ですが,実は以下のような得点状況だとします.このとき,試しにt検定を行ってみます.
data # score (Male) score (Female) 1 360 430 2 380 470 3 430 380 4 420 420 5 410 400 - グラフの作成
授業の最初の頃に行った棒グラフに誤差範囲を表示させる方法で,男女別得点のグラフを作成しましょう.
データ系列を選択して「Y誤差範囲挿入」でしたね.
- t 値の算出
まずは手作業で求めてみましょう.資料の(4)式に従って t 0を求めます.残差の平方和 Sx と Sy の求め方は以前にやりました.各データの自乗の和から各データの和の自乗/データ数を引く,でした.
- t分布表
t分布表をまずは自分で作ってみましょう.自由度は(4)式にもあるように nx + ny -2なので8になります.自由度8の危険率の計算をします. tinv()関数を使用します.
ところで,危険率とは資料に書いてあるように,求めた t 0 の値がt分布の両端のどの部分に入っているかを示すαという量で表されます.統計的には,求めた値が確率密度のグラフの端の方(確率的には5%未満のエリア)に入っている時,偶然生じたものではなくある意味を持っていると解釈します.このエリアの中でも更に端の方ほど偶然でない確率が高まります.そのため,だいたい10%と5%,そして1%などが基準になります.これは両側の確率なので,片側はそれぞれ半分ですから,5%という時には2.5%ずつ,ということになります.
tinv() 関数にそれぞれのαと自由度8を入れると,以下の表のようになるはずです.
α .10 .05 .01 t 1.8595 2.3060 3.3554 - 検定
資料のp.2の下半分からp.3にかけての説明を参考に今回の例で t 検定を行ってみましょう.
- グラフの作成
- t 検定用の関数
Excelにはt検定を行う関数 t.test() が用意されています.引数仕様がややこしいので,注意してください.
t.test(配列1,配列2,検定の指定,検定の種類) 各引数の意味は次のようになります.
配列1 配列2 検定の指定 検定の種類 1つ目のデータ範囲 2つ目のデータ範囲 1:片側確率
2:両側確率1:対応のあるデータ
2:2つの母集団の分散が等しい場合
3:2つの母集団の分散が等しくない場合
(ウェルチの手法)まず,片側か両側かですが,あるデータの平均値が別のデータの平均値よりも大きいかだけ,もしくは,小さいかだけを検定する場合には片側検定となります.t分布の右端もしくは左端の5%部分に入っているかどうかを見ます.一方,両側検定の場合には大きいか小さいかに関係なく,異なっているかを考えます.ですので,t分布の両側2.5%ずつのエリアに入っているかどうかを見ます.
次にタイプのところにある3つの分類ですが,1の対応のあるデータとは一人の人が2回試行してその間に違いがあるか,のような場合です.2つの群のデータを見る場合は通常は2の分散が等しい仮定で実施します.3は分散が異なることが予想される場合ですが,こちらは必要に応じて出てきたら説明します.
t.test() の実行結果は一つの数値で返ってきます.その数値は危険率と呼ばれるものになっており,通常はアルファベットの p (小文字)で示されます.資料の方に簡単に説明がありますが,2つの平均値に差がないとする帰無仮説を否定するときに間違っている確率です.先程も書きましたが,通常は5%未満になると,帰無仮説を棄却しても良いということになり,2つの平均値の間には有意な差があるとしてもよいことになっています.
TOEICのスコア 検定結果 男子学生の平均点:400点 女子学生の平均点:420点 帰無仮説:両者の平均点には有意な差は無い 対立仮説:両者の平均点には有意な差がある t 検定の結果: 危険率 p = .3466 (Φ = 8) よって帰無仮説を棄却できない(対立仮説は棄却された) 結論:両者の平均点には有意な差は無い
もし,危険率が5%未満だった場合には,結論のところに例えば以下のように記述します.
まず帰無仮説を立て,そして帰無仮説が否定できるかを確認する,という作業は面倒なように思えるでしょうが,検定の非対称性のために,必要な手順です.ざっくり言うと,仮説が違うということは p の値から言えますが,仮説が正しいことは検定によっては証明できないことに難しいところがあります.こちらのサイトなども参考にしてください.
結論:両者の平均点には有意な差がある (p = .0**, Φ = **) [注: ** は適当な数値] - 実際の検定
昨年度のJ1リーグのデータを使って検定を行ってみましょう.リンク先のデータは昨シーズンの各節のゴール数と勝利数をホームチームとアウェイチームとに分けて集計したものです.サッカーではホームチームが有利とよく言われますが,実際にどうなのかこのデータを使用して見てみましょう.
各節ごとの値の平均値を標準偏差をつけてグラフで表示すると以下のようになります.
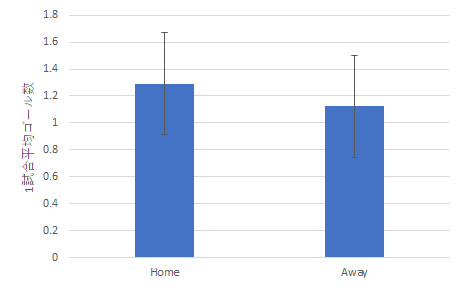
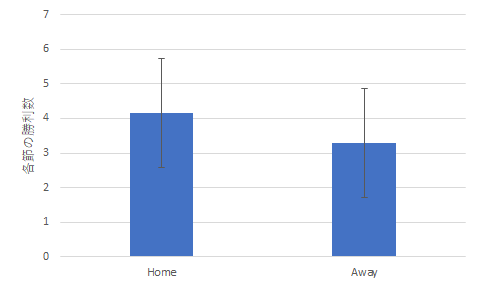
ゴール数の比較 勝利数の比較 今回の上のグラフは後で示すようにエラーバーをつけることをあらかじめ想定しています.そのため,グラフの枠線があると見づらくなることもあるので,枠線はなしとしています.
このようなエラーバーつきのグラフに慣れてくると,棒グラフの高さとエラーバーの重なり具合で検定結果がある程度予想できるようになります.目安はエラーバーとどれくらいかぶっているか,ということです.
Excelでグラフを作成する際に,グラフを右クリックして出て来るコンテクストメニューの上にある「枠線」アイコンの右の下向き記号 (∨) をクリックして,「枠線なし」を選ぶと枠線を消すことができます.さて,実際に t.test() 関数を使用して t 検定を行ってみましょう.ホームチームの数値の方が必ず大きいか,だけを問うのであれば片側検定でも良いのですが,一応違いがあるかどうかということを見る必要もあるので,両側検定ということにします.検定結果は危険率 p 値で表示され,今回のデータではそれぞれ 0.061 と 0.019 となるはずです.ゴール数の方は,p > .05 なので有意な差があるとは言えませんでした.なお,p < .10 の場合には「有意傾向がある」という表現を使う場合もあります.一方,勝利数の方は p < .05 なので,有意差があったということが言えるようです.ホームチームは基本的に有利であるということがJリーグでも観測されているようです.
なお,検定の結果を棒グラフでも表現してみてください.例えば,上で行ったTOEICの点数の場合ですと,有意差はありませんでした.その場合には棒グラフの上の方に有意差なしを表すn.s.というシンボルと線を表示します. n.s.とは not significant の略です. 有意傾向があることを言いたい場合には † (ダガー,短剣)記号をつけることがあります. 0.1% 未満の危険率で有意差がある場合には *** とアスタリスク3個, 1% 未満だとアスタリスク2個で ** , 5% 未満で1個 * と記号をつけます.
Offfice365にはドローソフトがありません.上のような作業をするのに一番近い機能を持っているのはPowerPointということになりそうです.PowerPointを起動して白紙のプレゼンテーションを選び,ペーストして作業をしてください.なお,折れ曲がる線を描画する機能もありませんので,直線を3本引いてなべぶた型の線を作りましょう.そのとき,例えば最初に左側の短い縦棒を作ったとすると,次にその線をコピーし,メニューバーにある「配置」から「配置」を選択して「上揃え」で高さを揃え,2本の縦線の位置をグラフ上でいい感じに配置した後,横棒を引きます.縦線や横線を引く時,Shiftキーを押したまま作業すると,垂直か水平もしくは45°の線になりますので,作業がやりやすくなります.
3本の線を引き終わったら,それら3本の線を選択して,「配置」から「グループ化」を選ぶと,一つの図形として以後は扱うことができますので,移動させた際にバラバラになったりすることを防げます.
n.s. や * などの入力は「挿入」メニューから「テキストボックス」を選ぶなどしてできます.
検定結果
- ゴール数
ホームチームの平均ゴール数 1.29 アウェイチームの平均ゴール数 1.12 帰無仮説:ホームチームとアウェイチームの得点数には有意な差はない 対立仮説:上記の得点数には有意な差がある t検定の結果:危険率 p = .0606 (Φ = 36) よって帰無仮説を棄却できない 結論:ホームチームとアウェイチームのゴール数には有意な差は無い(有意傾向にはあると言える)
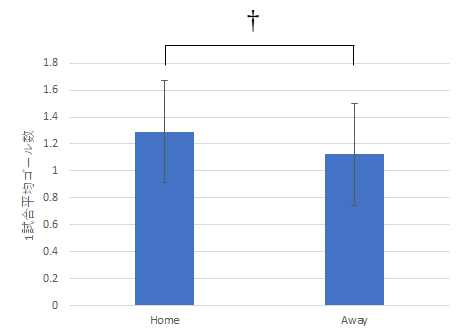
- 勝利数
ホームチームの平均勝利数 4.16 アウェイチームの平均勝利数 3.29 帰無仮説:ホームチームとアウェイチームの勝利数には有意な差はない 対立仮説:上記の勝利数には有意な差がある t検定の結果:危険率 p = .0192 (Φ = 36) よって帰無仮説は棄却可能 結論:ホームチームとアウェイチームの勝利数には有意な差がある (ホームチームの平均勝利数はアウェイチームの平均勝利数よりも多い)
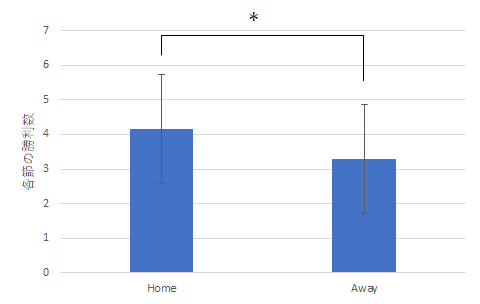
- ゴール数
- 次回の予習範囲
さて,今回は悲惨なことになってしまいました.分かっている人は分かっているんだけど,そうでない人は全然できていない状態でした.0点続出です.
まず,解答から行きましょう.結果としてのグラフは以下のようになります.
|
|

|
・・・ (1) |
問題用紙にもあるように式(1)は横軸に ID を取り,縦軸に時間でプロットすると,単純な直線の式,
T = a + b x
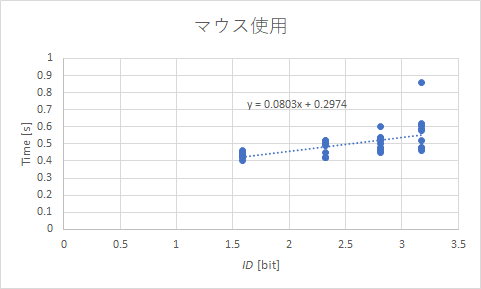
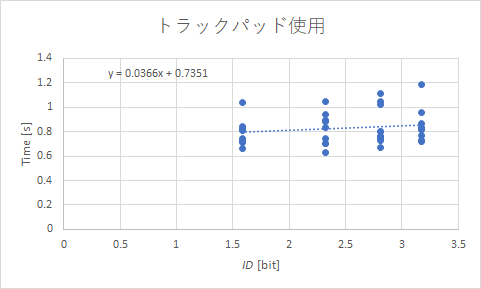
となりますので,近似曲線として線形を選べばそれで数式はすぐに出ます.図中にあるように簡単に求められます.その数値を使用すると,以下のようにまとめられます.
| デバイス | クリック時間 a [s] | b [s/bit] | 性能指数 IP [bit/s] |
|---|---|---|---|
| マウス | 0.297 | 0.0803 | 12.45 |
| トラックパッド | 0.735 | 0.0366 | 27.32 |
この実験は実はそこまで厳密に行っているわけでは無いので,統制が取れていない部分もあります.マウスやトラックボールの反応(C / D 比)の調整や,マウスの操作スペースの広さなどがいい加減です.それでも上の結果をまとめると,トラックパッドをタップするスピードはマウスクリックよりも遅いことと,マウスでカーソルを動かすよりも,狭いトラックパッドでカーソルを動かす方が速いことはわかりました.
なお,今回の実験のような値が縦に大きくばらつく結果を見たことが無いという人もいたかもしれませんが,Fittsの法則の実験はだいたいこんな感じです.
さて,問題のあるものを見ていきましょう.まずは,横軸が ID になっていない例です.さらにフィットさせる曲線も直線になっていません.
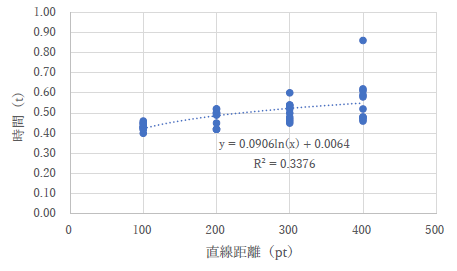
下のグラフは縦軸と横軸のラベル(説明)は合っているものの,実際には値が反対に入れ替わっていますね.
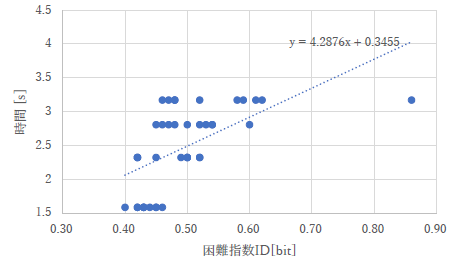
せっかくちゃんとグラフは描けたのに,近似曲線が間違っている人もいました.なぜ横軸に最初から ID を取るかというと,直線で近似できるようになるから,です.そのために説明しているのに,どうしてこういうことになるのでしょうか.
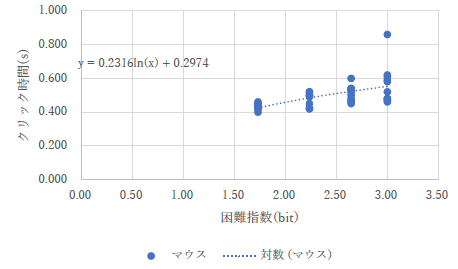
最後の下のものは,グラフのプロットまではいいのに,直線が原点を通るものとなってしまっています.それでは定数項の値を得ることができませんね.
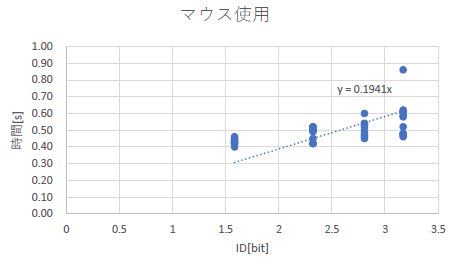
そして,残念なことに,今回も有効数字がおかしかったり,単位がなかったりしたものが出てきました.そうならないようにチェックシートを準備しているのに,無視して出しているのでしょうか.チェックシートを設問[4]としてつけるよう指示しているのに,無い人が大半です.特に今回は単位が無い人が大量に出てきました.困ったものですね.
前回は最小二乗法でした.今後は学生実験のデータ整理などでも活用してください.グラフに数式で表現される関係が背後にあることがわかっている場合には,どんどん使ってみてください.手計算しなくても,コンピュータを使えば簡単にできることがわかったと思います.
また,宿題で扱ったように,一見難しい関係式も変数変換により直線近似が可能になる場合がありますので,こちらも学生実験で出てきた時には活用してください.
資料を参考に予習してください.
今回はt検定について学習します.t検定とは2つの平均値の違いを統計的に調べるものです.例えば,ある大学のある学科の男子学生と女子学生のTOEICの平均値がそれぞれ400と420だったとします.このとき,女子学生の集団のほうがTOEICの点数が「高い」と言えるでしょうか?もちろん,平均値は女子学生の方が高かったことは確かです.しかし,その違いに「意味がある」のでしょうか.このような2つの平均値の差に意味があるのかどうかを「検定」するのがt検定です.
次回は相関係数について学習します.予習用の資料を参考に予習してください.
いつものレポート提出システムを利用して行います.
宿題の公開は原則として水曜日の18:00からとなります.また,提出の締め切りは授業翌週の火曜日の13:00です.よろしくお願いします.
Back