身近な最適制御の話

面白い電子制御の話

身近な最適制御の話

2001.2.7
制御システム工学　　　吉田和信

1. はじめに

　制御工学では，現在の出力（結果）が過去の入力（原因）にも依存するシステム，すなわち，動的システムの制御問題を扱う． 過去に無関係に存在するものはないので，その意味では，世の中のあらゆる対象は動的システムであるといえる．
　入出力関係（因果関係）を数式で表した数学モデルが得られれば，原理的には，所望の出力を発生させる入力を計算することができる． 特に，ある規範に対して，最良の出力を生ずる入力を最適制御という． 遭遇する問題に対して，より良い結果を出すように努力することが人類共通の課題であろうが，対象のモデルが明確でなければ，試行錯誤を伴うことになる． 例えば，社会，経済システムのように大規模・複雑なシステムでは，評価基準が与えられたとしても，モデルがよくわからないので，最適な政治方針，経済方針の決定が困難となる．
　ここでは，工学における比較的簡単な対象に絞って，最適制御問題とその解を紹介する．最適制御問題は，数学モデルが既知の場合でも解を求めるのが難しく，通常，最大原理や動的計画法という数学的手法を用いて，コンピュータを用いた数値計算によって解かれる．最適制御の多くは，日常経験から類推することのできないような意外な形をとる．


2.　水槽系の最短時間制御



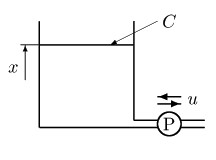
図１：水槽系


　図1に示す断面積 C の水槽系を考える．水槽に結合された管にはポンプが取り付けてあり，水を給排水できる構造になっている． u は流量であり，その符号を流出のとき負，流入のとき正とする． 空の水槽に対して，最短時間で水位 1m まで x を制御する u(t) を求めるという最短時間制御問題を考えよう． ただし， C = 1m2 とし， u には

| u |≦1m3/s




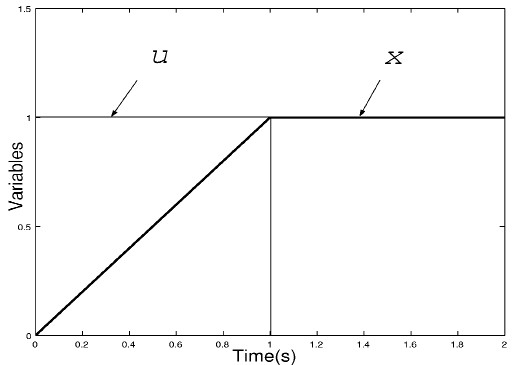
図２：水槽系の最短時間制御


という制限があるものとする．
　図2に制御結果を示す．すなわち，時刻 0 で u を最大流量にセットし，水位が所望のレベルに達した瞬間に 0 に戻すという制御が，この場合の最適制御である． お風呂やバケツに最短時間で水をためたい場合，このような制御を行えばよい．これは，日常経験からも解がわかる例である．


3.　慣性系の最短時間制御




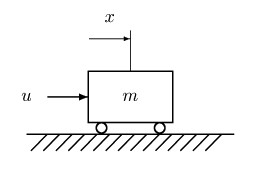
図３：慣性系


　つぎに，図3の慣性系を考えよう．質量 m をもつ物体の位置を x とする．物体には，力 u を加えることができる． 静止した物体を x = 0 から， x = 1 まで最短時間で移動させ，そこで止める制御 u(t)を求める問題を考える．ただし， u = 1 とし， u には

| u |≦ 1

なる制限があるものとする（各変数は適当な単位をもつ）．




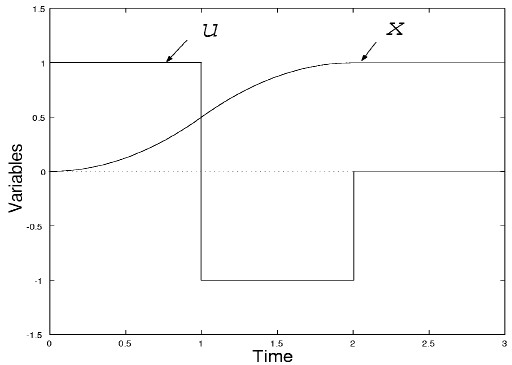
図４：慣性系の最短時間制御


　図4に最適制御結果を示す． x の目標位置の半分までは，正の最大加速度で，残り半分は負の最大加速度で制御されている． 一般に，入力 u に制限がある場合の最適制御は，常に，最大値または最小値をとるという特徴がある． このような制御をバンバン制御という．慣性系の場合，最適制御は，１回までの切り換えをもつ．
　目標値で止まることを要求するから，負の最大加速度も等しい割合で使うことになる． もし，目標値を最短時間で通過すればよいという問題設定にすれば，水槽系の最適制御と同様に，最初から最後まで最大入力で制御するという解となる．


4. 1自由度振動系の最短時間制御



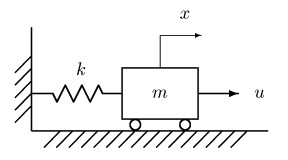
図５：1自由度振動系


　今度は，図5の1自由度振動系に対する最短時間制御問題を考えよう． m,k,x,u は，それぞれ，物体の質量，ばね係数，物体の位置，入力（力）を表す． 問題は，初期振動があるとして，最短時間で物体の振動を止める（ x = dx/dt = 0 とする）ことである．具体的には， m = 1, k = 1 とし， u には，上の問題同様

| u |≦ 1

という制限が課せられているとする．




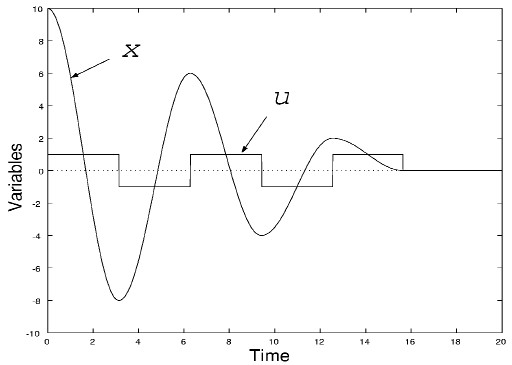
図６：1自由度振動系の最短時間制御


　図6は，物体の初期位置を x(0) = 10 とした場合の最適制御である．バンバン制御が行われているのは，これまでの例と同じであるが，振動系の場合，最適制御の切り換え回数は初期値に依存し，初期値が大きくなれば，切り換え回数も多くなる． また，切り換え時刻は，もはや簡単なルールから決めることができなくなる．


5.　可変長振り子系（ブランコ）の最適制御




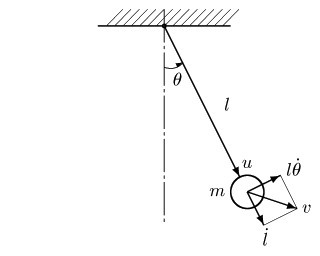
図７：可変長振り子系


　図7の可変長振り子系を考えよう．図において，θは振り子の振れ角， l は支点から重りまでの距離， m は重りの質量， u は重りの駆動力である．振り子の棒の質量は無視する。 l はつぎの制限を受けるものとする．

0 < l0 ≦ l ≦ l1

問題は， l の制限のもとで，振り子系の振動を速やかに減衰させる l の制御則を求めることである．




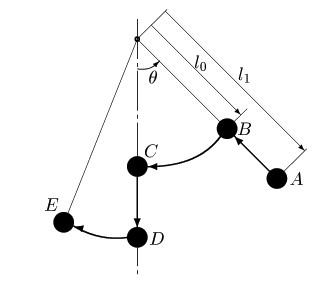
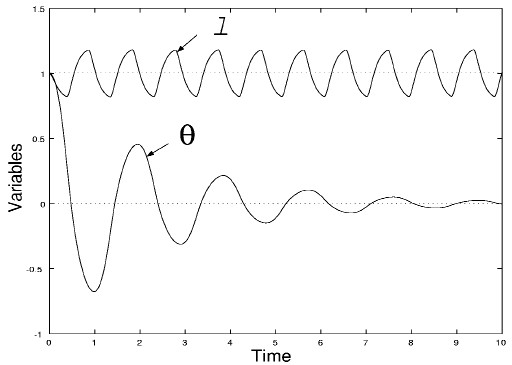
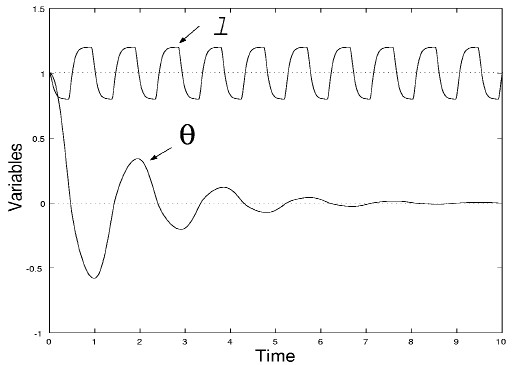
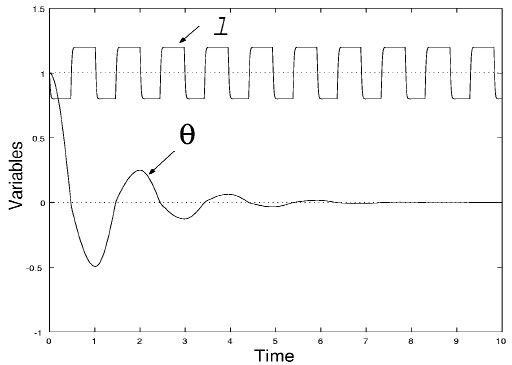
図８：最適制御


　振り子振動の減衰を最大にする最適制御は，図8に示すように，振り子長をθ = 0 のとき l0 から l1 へ， dθ/dt = 0 のとき l1 から l0 へ瞬間的に移動する制御である．実際には，このように重りを瞬間的に移動する制御の実現は不可能であるが，これを近似的に行う制御系をシミュレーションしてみよう． 図9〜図11にシミュレーション結果を示す． T は，重りを移動するサーボ系の時定数を表す（ T が小さいほど，重りの移動が速い）． 図9，10，11の順に最適制御を近似している．また，この順に振動の減衰率が向上しているのもわかる． 一方，図8の制御の逆パターンは，振り子振動を最も効果的に増幅する最適制御となる．
　振り子の振動問題は古くから考察されているが，このような制御が最適振動制御になることが明示されたのは比較的最近（1993）のことである． シミュレーションで示したようにある程度最適制御を近似していれば，制御系は安定となる（振動の振幅が減衰する）． 最適制御をどの程度近似すれば安定であるかという定量的条件は文献3.に示されている．




図9 可変長振り子系の制御（ T = 0.1）





図10 可変長振り子系の制御（ T = 0.05）





図11 可変長振り子系の制御（ T = 0.01）



6.　おわりに

　最適制御は，一般に，バンバン制御の形をとり，実現不可能な場合もある． また，制御系に要求される性質として，ロバスト性（対象の変化や外的要因による擾乱があっても，安定性などの制御性能があまり劣化しない性質）があるが，制御性能の向上とロバスト性の向上は両立しないという宿命があり，制御性能を最適化した最適制御は，良好なロバスト性をもたない． それでも，実際，最適制御を行うかどうかは別として，制御性能の限界を知ることは意義深い．


7.　参考文献

  1. E.P.Ryan : Optimal relay and saturating control system synthesis, PETER PEREGRINUS LTD.(1982)
  2. E.K.Lavrovskii and A.M.Formalskii : Optimal control of the pumping and damping of a swing, Journal of Applied Mathematics and Mechanics, Vol.57, No.2, pp.311--320(1993)
  3. 吉田和信，川辺尚志，西村行雄：重心移動による振子系の振動制御，システム制御情報学会論文誌，Vol.13, No.10, pp.470--477(2000)
面白い話の目次へ戻る